《2025年北大绿卡九年级数学下册人教版》

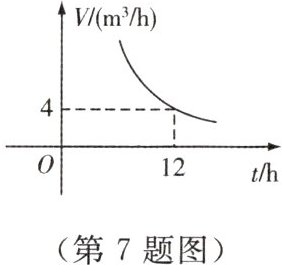
7. 如图所示的是一蓄水池的排水量$V(m^{3}/h)$与排完水池中的水所用的时间$t$(h)之间的函数关系图象.
(1)写出此函数解析式；
(2)如果要6 h排完水池中的水，那么每小时的排水量应该是多少?

答案： 【解】
(1)由图象可知该函数为反比例函数。
设函数解析式为$V = \frac{k}{t}(k\neq0)$，
则$k = 4×12 = 48$，
∴此函数的解析式为$V = \frac{48}{t}$。
(2)当$t = 6$时，$V = \frac{48}{6} = 8$。
故每小时的排水量应为$8\ m^{3}$。

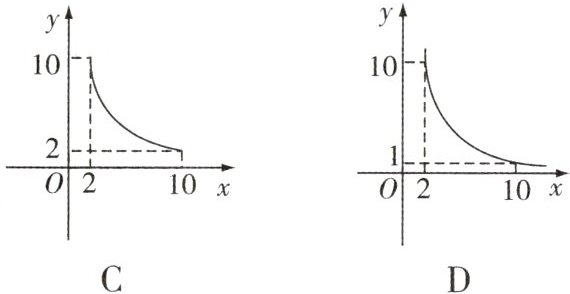
8. 如图，一张正方形的纸片，剪去两个一样的小矩形得到一个“E”形图案.设小矩形的长、宽分别为$x$，$y$，剪去部分的面积为20，若$2\leqslant x\leqslant10$，则$y$关于$x$的函数图象是( )．

答案： A

9. 菱形的面积为$12\ cm^{2}$，两条对角线的长分别为$x\ cm$和$y\ cm$，则$y$与$x$之间的函数关系式为_______，当其中一条对角线的长为6 cm时，另一条对角线的长为_______cm.

答案： $y = \frac{24}{x}$ 4

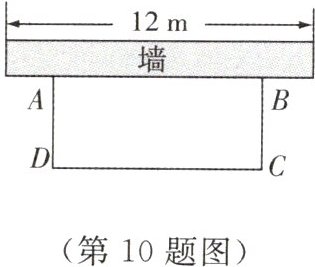
10. 如图，某科技小组准备用材料围建一个面积为$60\ m^{2}$的矩形科技园$ABCD$，其中一边$AB$靠墙，墙长为12 m，设$AD$的长为$x\ m$，$DC$的长为$y\ m$.
(1)求$y$与$x$之间的函数关系式；
(2)若围成矩形科技园$ABCD$的三边材料总长不超过26 m，材料$AD$和$DC$的长都是整米数，求出满足条件的所有围建方案.

答案： 【解】
(1)由题意得$S_{矩形ABCD}=AD\cdot DC = xy = 60$，
故$y = \frac{60}{x}(x\geq5)$。
(2)由$y = \frac{60}{x}$且$x$，$y$都是正整数，可得$x$取 1，2，3，4，5，6，10，12，15，20，30，60。
∵$2x + y\leq26$，$0 ＜ y\leq12$，
∴符合条件的围建方案为：①$AD = 5\ m$，$DC = 12\ m$；②$AD = 6\ m$，$DC = 10\ m$；③$AD = 10\ m$，$DC = 6\ m$。