《2025年北大绿卡九年级数学下册人教版》

9 下列网格中各个小正方形的边长均为1，阴影部分图形分别记作甲、乙、丙、丁，其中是相似图形的为( ).

A. 甲和乙
B. 乙和丁
C. 甲和丙
D. 甲和丁

答案： D

10 有四组线段，每组线段长度如下：①2,1,$\sqrt{2}$,$\sqrt{2}$；②3,2,9,6；③$\frac{1}{2}$,1,$\sqrt{5}$,$\sqrt{2}$；④1,3,5,7. 其中是成比例线段的有( ).
A. 1组
B. 2组
C. 3组
D. 4组

答案： B

11 如图，线段A₁B₁，B₁C₁，A₂B₂，B₂C₂的端点都在边长为1的小正方形的顶点上，这四条线段是成比例线段吗？为什么？

答案： 【解】成比例. 理由如下：
$\because A_{1}B_{1}=\sqrt{2^{2}+2^{2}} = 2\sqrt{2}$，$B_{1}C_{1}=\sqrt{2^{2}+6^{2}} = 2\sqrt{10}$，
$A_{2}B_{2}=\sqrt{1^{2}+1^{2}}=\sqrt{2}$，$B_{2}C_{2}=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，
$\therefore\frac{A_{1}B_{1}}{A_{2}B_{2}}=\frac{2\sqrt{2}}{\sqrt{2}} = 2$，$\frac{B_{1}C_{1}}{B_{2}C_{2}}=\frac{2\sqrt{10}}{\sqrt{10}} = 2$，
$\therefore\frac{A_{1}B_{1}}{A_{2}B_{2}}=\frac{B_{1}C_{1}}{B_{2}C_{2}}$，
$\therefore$线段$A_{1}B_{1}$，$B_{1}C_{1}$，$A_{2}B_{2}$，$B_{2}C_{2}$成比例。

12 如图，正五边形FGHMN与正五边形ABCDE相似，若AB：FG = 2：3，则下列结论正确的是( ).

A. 2DE = 3MN
B. 3DE = 2MN
C. 3∠A = 2∠F
D. 2∠A = 3∠F

答案： B

13 如图，取一张长为a，宽为b的矩形纸片，将它对折两次后得到一张小矩形纸片，若要使小矩形纸片与原矩形纸片相似，则a：b = ________.

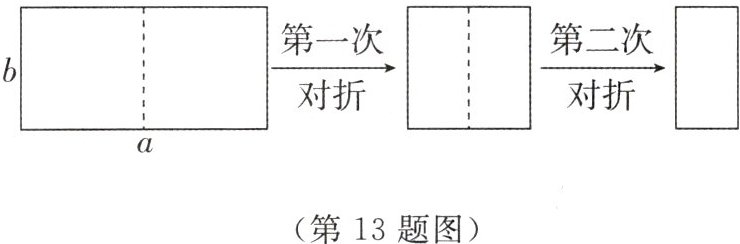
答案： $2:1$ 【解析】对折两次后得到的小矩形纸片的长为$b$，宽为$\frac{1}{4}a$，
$\because$小矩形纸片与原矩形纸片相似，
$\therefore\frac{a}{b}=\frac{b}{\frac{1}{4}a}$。
又$\because a＞0$，$b＞0$，
$\therefore\frac{a}{b}=2$，即$a:b = 2:1$。
故答案为$2:1$。

14 如图，DE//BC且△ADE与△ABC相似，试求两个三角形中未知边DE和AC的长.

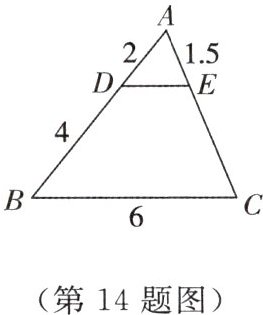
答案： 【解】由题意，得$\frac{AD}{AB}=\frac{DE}{BC}=\frac{AE}{AC}$，
$\therefore\frac{2}{2 + 4}=\frac{DE}{6}=\frac{1.5}{AC}$，
$\therefore DE = 2$，$AC = 4.5$。

15 如图，已知∠1' = ∠1，∠2' = ∠2，∠3' = ∠3，∠4' = ∠4，∠D' = ∠D，试判断四边形A'B'C'D'与四边形ABCD是否相似，并说明理由.

答案： 【解】四边形$ABCD$与四边形$A'B'C'D'$相似.
理由：由已知条件知$\angle DAB=\angle D'A'B'$，$\angle B=\angle B'$，$\angle BCD=\angle B'C'D'$，$\angle D=\angle D'$，
且$\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CD}{C'D'}=\frac{DA}{D'A'}=\frac{5}{6}$，
所以四边形$ABCD$与四边形$A'B'C'D'$相似。