《2025年小题狂做高中物理必修第二册人教版》

1. [2025 重庆江北期中]在物理学发展的过程中，科学家总结了许多重要的物理思想与方法。关于物理学思想方法和物理学史，下列叙述正确的是(B)

A.探究向心力大小与半径、角速度、质量的关系实验中，采用了等效替代的思想
B.卡文迪什在测万有引力常量时，利用了微小量放大法的思想
C.第谷在其天文观测数据的基础上，总结出了行星按照椭圆轨道运行的规律
D.牛顿发现了万有引力定律，并通过扭秤实验测出了引力常量的数值

答案： 1.B 探究向心力大小与半径、角速度、质量的关系实验中，采用了控制变量法，A错误；卡文迪什在测万有引力常量时，利用了微小量放大法的思想，B正确；开普勒在第谷天文观测数据的基础上，总结出了行星按照椭圆轨道运行的规律，C错误；牛顿发现了万有引力定律，卡文迪什通过扭秤实验测出了引力常量的数值，D错误.

2. “祝融号”火星车需要“休眠”以度过火星寒冷的冬季。假设火星和地球的冬季是各自公转周期的四分之一，且火星的冬季时长约为地球的 1.88 倍。火星和地球绕太阳的公转均可视为匀速圆周运动。下列关于火星、地球公转的说法正确的是(D)

A.火星公转的线速度比地球的大
B.火星公转的角速度比地球的大
C.火星公转的半径比地球的小
D.火星公转的加速度比地球的小

答案： 2.D 由题意可知，火星的公转周期大于地球的公转周期，根据$G\frac{Mm}{r^{2}}=m\frac{4\pi^{2}}{T^{2}}r$可得$T = 2\pi\sqrt{\frac{r^{3}}{GM}}$，可知火星的公转半径大于地球的公转半径，故C错误；根据$G\frac{Mm}{r^{2}}=m\frac{v^{2}}{r}$可得$v=\sqrt{\frac{GM}{r}}$，可知火星的公转线速度小于地球的公转线速度，故A错误；根据$\omega=\frac{2\pi}{T}$可知火星公转的角速度小于地球公转的角速度，故B错误；根据$G\frac{Mm}{r^{2}}=ma$可得$a=\frac{GM}{r^{2}}$，可知火星公转的加速度小于地球公转的加速度，故D正确.
快速解题 根据口诀“高轨低速（‘速’包含线速度、加速度和向心加速度）大周期，低轨（$r$小）高速小周期”可快速解题.

3. [2025 江苏泰州期中]2024 年 6 月，“嫦娥六号”实现世界首次月球背面自动采样返回，采回样品质量 1 935.3 g。已知月球和地球的质量之比为 a，半径之比为 b，所采样品在月球与在地球上的重力之比为(D)

A.$\frac{a}{b}$
B.$\frac{a}{b}$
C.$\frac{b^{2}}{a}$
D.$\frac{a}{b^{2}}$

答案： 3.D 由万有引力等于重力有$\frac{GMm}{R^{2}}=mg$，解得星球表面的重力加速度为$g = \frac{GM}{R^{2}}$，则月球与地球的表面的重力加速度之比为$\frac{g_{月}}{g_{地}}=\frac{a}{b^{2}}$，则所采样品在月球与在地球上的重力之比为$\frac{a}{b^{2}}$，故D正确.

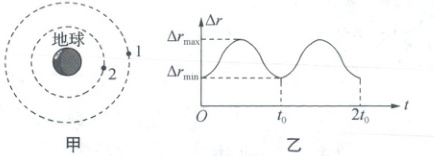
4. [2025 云南模拟]如图甲所示，两颗人造地球卫星 1、2 在同一平面内沿同一方向绕地球做圆周运动，周期分别为 $T_{1}$、$T_{2}$，轨道半径分别为 $r_{1}$、$r_{2}$。某时刻开始计时，两卫星间距 $\Delta r$ 随时间 $t$ 变化的关系如图乙所示，已知 $t_{0}=\frac{1}{7}T_{1}$，则 $\frac{r_{1}}{r_{2}}$ 等于(B)

A.2
B.4
C.6
D.8

答案： 4.B 根据图像可知，经过时间$t_{0}$两卫星再次相距最近，则有$\frac{2\pi}{T_{2}}t_{0}-\frac{2\pi}{T_{1}}t_{0}=2\pi$，根据题意有$t_{0}=\frac{1}{7}T_{1}$，解得$T_{2}=\frac{1}{8}T_{1}$，根据开普勒第三定律有$\frac{r_{1}^{3}}{T_{1}^{2}}=\frac{r_{2}^{3}}{T_{2}^{2}}$，解得$\frac{r_{1}}{r_{2}}=4$，故B正确.

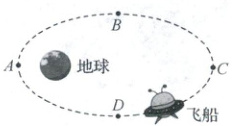
5. [2025 广东佛山阶段练习]如图所示，神舟十七号载人飞船绕地球沿椭圆轨道运动，运动周期为 $T$，图中虚线为飞船的运行轨迹，$A$、$B$、$C$、$D$ 是轨迹上的四个位置，其中 $A$ 点距离地球最近，$C$ 点距离地球最远。$B$ 点和 $D$ 点是弧线 $ABC$ 和 $ADC$ 的中点，下列说法正确的是(D)


A.飞船在 $C$ 点所受地球引力最大
B.飞船在 $A$ 点运行速度最小
C.飞船从 $B$ 点经 $C$ 到 $D$ 点的运动时间为 $\frac{T}{2}$
D.若用 $r$ 代表椭圆轨道的半长轴，$T$ 代表飞船运动周期，则 $\frac{r^{3}}{T^{2}}=k$，神舟十七号飞船和月球绕地球运行对应的 $k$ 值相等

答案： 5.D 根据$F = G\frac{Mm}{r^{2}}$可知飞船在A点所受地球引力最大，A错误；根据开普勒第二定律可知，飞船在A点运行速度最大，B错误；因为飞船从A点到C点速度逐渐减小，从C点到A点速度逐渐增大，故飞船从B点经C到D点的运动时间大于$\frac{T}{2}$，C错误；若用$r$代表椭圆轨道的半长轴，$T$代表飞船运动周期，则$\frac{r^{3}}{T^{2}}=k$，根据开普勒第三定律，神舟十七号飞船和月球绕地球运行对应的$k$值相等，D正确.

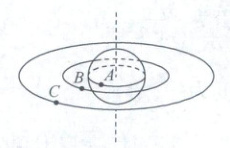
6. [2025 黑龙江哈尔滨月考]如图所示，$A$ 是静止在赤道上的物体，$B$、$C$ 是同一平面内两颗人造卫星。$B$ 位于离地高度等于地球半径的圆形轨道上，$C$ 是地球静止卫星。已知地球自转周期为 $T_{1}$，$B$ 的运行周期为 $T_{2}$，则以下判断正确的是(D)


A.卫星 $C$ 的运行速度大小大于地球的第一宇宙速度
B.$A$、$B$ 的线速度大小关系为 $v_{A}＞v_{B}$
C.周期大小关系为 $T_{C}＞T_{B}＞T_{A}$
D.$B$、$C$ 相距最近为计时起点，绕行方向相同，经过时间 $\frac{T_{1}T_{2}}{2(T_{1}-T_{2})}$，$B$、$C$ 相距最远

答案： 6.D 根据$G\frac{Mm}{r^{2}}=m\frac{v^{2}}{r}$，解得$v=\sqrt{\frac{GM}{r}}$，可知轨道半径越大，线速度越小，第一宇宙速度等于近地卫星的环绕速度，其轨道半径最小，可知，卫星C的运行速度大小小于地球的第一宇宙速度，A错误；结合上述可知，B的线速度大于C的线速度，同步卫星与地球自转角速度相等，根据$v = \omega r$可知，C的线速度大于A的线速度，则有$v_{A}＜v_{B}$，B错误；根据$G\frac{Mm}{r^{2}}=\frac{4\pi^{2}r}{T^{2}}$，解得$T=\sqrt{\frac{4\pi^{2}r^{3}}{GM}}$，可知C的周期大于B的周期，又由于同步卫星的周期等于地球自转周期，则有$T_{C}=T_{A}＞T_{B}$，C错误；C相距最近为计时起点，绕行方向相同，则B、C第一次相距最远时有$\frac{2\pi}{T_{2}}\Delta t-\frac{2\pi}{T_{1}}\Delta t=\pi$，解得$\Delta t=\frac{T_{1}T_{2}}{2(T_{1}-T_{2})}$，D正确.