《2025年小题狂做高中物理必修第二册人教版》

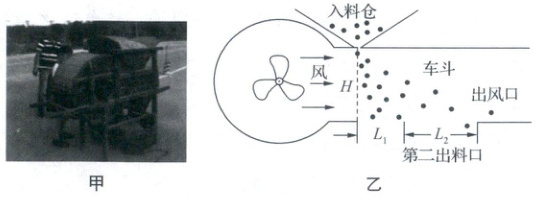
14. [2024 湖南长沙期中]如图甲所示为风谷车（又称风车），我国农业种植中用来去除水稻等农作物子实中杂质、瘪粒、秸秆屑等的木制传统农具，其工作原理可简化为图乙所示：转动摇手柄，联动风箱内的风叶，向车斗内送风，装入入料仓的谷物中混有质量较大的饱粒和质量稍小的瘪粒，均无初速地从入料仓漏下，在车斗中下落高度 H = 0.45 m 后，从宽度为$L_1 = 0.18$ m 的第一出料口出来的都称之为饱粒，其中的最小质量为$1×10^{-4}$ kg；从宽度为$L_2$（待求）的第二出料口出来的都称之为瘪粒，其中的最小质量为$5×10^{-5}$ kg；质量小于$5×10^{-5}$ kg 的草屑被吹出出风口. 只考虑重力和水平风力 F（设每颗粒受到的水平风力都相同，不同颗粒的质量分布是连续的），g 取 10 m/s². 求：
（1）水平风力 F 的大小；
（2）第二出料口的宽度$L_2$.

答案： 14.
(1)谷物在竖直方向上做自由落体运动，根据自由落体运动规律$H = \frac{1}{2}gt^{2}，$解得t = 0.3s，设饱粒的最小质量为m，其对应落点在第一出料口的最右侧，水平方向做匀加速运动，有$L_{1} = \frac{1}{2}at^{2}，$解得$a = 4m/s^{2}，$根据牛顿第二定律有F = ma，解得$F = 4.0×10^{-4}N.$
(2)设瘪粒中质量最小的颗粒质量为m'，其对应落点在第二出料口最右侧，根据牛顿第二定律有F = m'a'，在水平方向做匀加速运动，则有$L_{1} + L_{2} = \frac{1}{2}a't^{2}，$联立解得$L_{2} = 0.18m.$

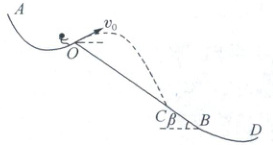
15. [2025 江西鹰潭一模]2025 年 2 月 10 日，鹰潭余江籍运动员杨文龙在哈尔滨亚冬会单板滑雪男子大跳台决赛中勇夺金牌. 如图为简化后的跳台滑雪雪道示意图，AO 段为助滑道和起跳区（倾角为α），OB 段为倾角为β的着陆坡，BD 为停止区. 运动员从助滑道的起点 A 由静止开始下滑，到达起跳点 O 时，借助设备和技巧，以与水平方向成α角（起跳角）的方向起跳，最后落在着陆坡面上的 C 点. 已知运动员在 O 点以$v_0$的速率起跳，轨迹如图虚线所示，不计一切阻力，重力加速度为 g. 求：

（1）运动员在空中运行的最小速度；
（2）运动员离开着陆坡面 OB 的最大距离；
（3）若α = β = 30°，运动员所到达的 C 点与起跳点 O 的距离.

答案： 15.
(1)建立水平和竖直坐标轴，不计阻力的情况下，运动员在空中做斜抛运动，水平方向做匀速运动，当竖直方向速度减到零的时候，速度最小，此时有$v_{min} = v_{0}\cos\alpha.$
(2)沿斜面和垂直于斜面建立坐标轴，速度分解有$v_{x} = v_{0}\cos(\alpha + \beta)，$$v_{y} = v_{0}\sin(\alpha + \beta)，$加速度分解有$g_{x} = g\sin\beta，$$g_{y} = g\cos\beta，$当$v_{y}$减到零时，运动员离着陆坡OB最远，有$2g_{y}H = v_{y}^{2}，$联立解得$H = \frac{v_{0}^{2}\sin^{2}(\alpha + \beta)}{2g\cos\beta}.$
(3)当运动员垂直于斜面OB的位移为零时落到C点，有$v_{y}t - \frac{1}{2}g_{y}t^{2} = 0，$解得t = 0(舍去)，$t = \frac{2v_{0}\sin(\alpha + \beta)}{g\cos\beta}，$所以运动员所到达的C点与起跳点O的距离$L = v_{x}t + \frac{1}{2}g_{x}t^{2} = \frac{2v_{0}^{2}}{g}.$