《2025年小题狂做高中物理必修第二册人教版》

8. “嫦娥”一号是我国首颗人造绕月卫星，具有重要意义。如图所示为“嫦娥”一号卫星撞月的模拟图，卫星从控制点开始沿撞月轨道在撞击点成功撞月。假设卫星绕月球做圆周运动的轨道半径为 $ r $，周期为 $ T $，引力常量为 $ G $，卫星在半径为 $ r $ 的绕月轨道上的重力加速度大小为 $ g $，月球半径为 $ R $，根据以上信息可计算月球的质量为(AD)


A.$ \frac{gr^{2}}{G} $
B.$ \frac{gR^{2}}{G} $
C.$ \frac{4\pi^{2}R^{3}}{GT^{2}} $
D.$ \frac{4\pi^{2}r^{3}}{GT^{2}} $

答案： 8.AD 根据万有引力提供向心力，有$\frac{GMm}{r^{2}} = m(\frac{2\pi}{T})^{2}r$，解得$M = \frac{4\pi^{2}r^{3}}{GT^{2}}$，C错误，D正确；在该轨道上有$\frac{GMm}{r^{2}} = mg$，解得$M = \frac{gr^{2}}{G}$，A正确，B错误.

9. [2024 湖南娄底月考]2023 年 9 月 21 日 15 时 48 分，中国空间站“天宫课堂”第四课正式开讲。新晋“太空教师”景海鹏、朱杨柱、桂海潮为广大青少年带来了一堂精彩的太空科普课，这是中国航天员首次在“梦天”实验舱内进行授课。已知地球半径为 $ R $，引力常量为 $ G $，若“梦天”实验舱做匀速圆周运动的轨道半径是地球半径的 $ k $ 倍，“梦天”实验舱与地球中心的连线在单位时间内扫过的面积为 $ S $，则下列说法正确的是(AD)

A.“梦天”实验舱的环绕周期为 $ \frac{\pi k^{2}R^{2}}{S} $
B.地球的质量为 $ \frac{3S^{2}}{GkR} $
C.“梦天”实验舱处的重力加速度大小为 $ \frac{4\pi S^{2}}{k^{3}R^{3}} $
D.地球的密度为 $ \frac{3S^{2}}{\pi kGR^{4}} $

答案： 9.AD 由几何关系得$S = \frac{\pi(kR)^{2}}{T}$，所以“梦天”实验舱的环绕周期为$T = \frac{\pi k^{2}R^{2}}{S}$，故A正确；由万有引力提供向心力，得$G\frac{Mm}{(kR)^{2}} = m\frac{4\pi^{2}}{T^{2}}kR$，解得地球的质量为$M = \frac{4S^{2}}{GkR}$，故B错误；由$\rho = \frac{M}{V}$、$V = \frac{4}{3}\pi R^{3}$，可得地球的密度为$\rho = \frac{3S^{2}}{\pi kGR^{3}}$，故D正确；由万有引力等于重力，得$G\frac{Mm}{(kR)^{2}} = mg$，所以“梦天”实验舱处的重力加速度大小为$g = \frac{4S^{2}}{k^{3}R^{3}}$，故C错误.

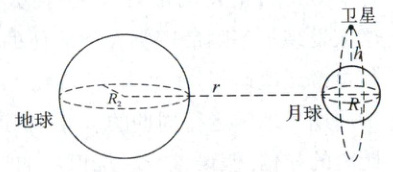
10. [山东济宁期中]我国发射的探月卫星有一类为绕月极地卫星，利用该卫星可对月球进行成像探测。如图所示，设卫星在绕月极地轨道上做圆周运动时距月球表面的高度为 $ h $，绕行周期为 $ T_{1} $；月球半径为 $ R_{1} $，公转轨道半径为 $ r $；地球半径为 $ R_{2} $，地球表面重力加速度为 $ g $，引力常量为 $ G $。忽略地球引力、太阳引力对绕月卫星的影响。求：
（1）月球质量 $ M_{1} $；
（2）月球绕地球公转的周期 $ T_{2} $。

答案： 10.
(1)卫星环绕月球做匀速圆周运动，可得$\frac{GM_{1}m}{(R_{1} + h)^{2}} = m(\frac{2\pi}{T_{1}})^{2}(R_{1} + h)$，解得月球质量$M_{1} = \frac{4\pi^{2}(R_{1} + h)^{3}}{GT_{1}^{2}}$.
(2)设地球质量为$M_{2}$，月球绕地球做匀速圆周运动，可得$\frac{GM_{1}M_{2}}{r^{2}} = M_{1}(\frac{2\pi}{T_{2}})^{2}r$，在地球表面有$\frac{GM_{2}m'}{R_{2}^{2}} = m'g$，联立解得$T_{2} = \frac{2\pi r}{R_{2}}\sqrt{\frac{r}{g}}$.

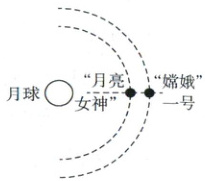
11. [2024 湖南岳阳期中]如图所示是“月亮女神”和“嫦娥”一号绕月球做圆周运动时某时刻的图片，用 $ r_{1} $、$ r_{2} $、$ T_{1} $、$ T_{2} $ 分别表示“月亮女神”和“嫦娥”一号的轨道半径及周期，用 $ R $ 表示月球的半径。
（1）请用万有引力知识证明：它们遵循 $ \frac{r_{1}^{3}}{T_{1}^{2}}=\frac{r_{2}^{3}}{T_{2}^{2}}=k $，其中 $ k $ 是只与月球质量有关而与卫星无关的常量。
（2）再经多少时间两卫星第一次相距最远？
（3）请用“嫦娥”一号所给的已知量，估测月球的平均密度。

答案： 11.
(1)设月球的质量为$M$，对任一卫星，由万有引力提供向心力，有$G\frac{Mm}{r^{2}} = m\frac{4\pi^{2}}{T^{2}}r$，解得$\frac{r^{3}}{T^{2}} = \frac{GM}{4\pi^{2}} = k$，为常量.
(2)设再经时间$t$两卫星第一次相距最远，有$\frac{2\pi t}{T_{1}} - \frac{2\pi t}{T_{2}} = \pi$，解得$t = \frac{T_{1}T_{2}}{2T_{2} - 2T_{1}}$.
(3)对“嫦娥”一号，由万有引力提供向心力，有$G\frac{Mm}{r_{2}^{2}} = m\frac{4\pi^{2}}{T_{2}^{2}}r_{2}$，又$M = \frac{4}{3}\pi R^{3}\rho$，联立解得$\rho = \frac{3\pi r_{2}^{3}}{GR^{3}T_{2}^{2}}$.