2026年一本密卷高考物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年一本密卷高考物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
58.某用电器额定电压为2.8V、额定功率为2.8×10−3W,为了研究其伏安特性,需要电压表和电流表,但
实验室可选用的器材只有;微安表(量程100μA,内阻900Ω);电阻箱R1(阻值范围0~999.9Ω);电阻
箱R2(阻值范围0~9999.9Ω);导线若干。回答下列问题:
(1)利用所给嚣材组装一个量程为1mA的直流电流表,需要________联一个阻值为________Ω的
电阻;
(2)能用所给微安表及一个电阻箱改装成一个量程为3V的电压表吗?如果能,如何改装?如果不能,
请说明理由。
_
(3)如果某同学先用所给器材组装一个量程为1mA的电流表,在此基础上再将它
改装成量程为3V的电压表。组装好的多用电表有电流量程1mA和电压量程
3V两挡。请你在右图虚线框内画出电路图并标出R1和R2,其中为公共接线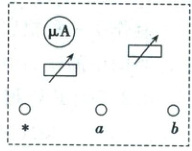
柱,a和b分别是电流挡和电压挡的接线柱。
实验室可选用的器材只有;微安表(量程100μA,内阻900Ω);电阻箱R1(阻值范围0~999.9Ω);电阻
箱R2(阻值范围0~9999.9Ω);导线若干。回答下列问题:
(1)利用所给嚣材组装一个量程为1mA的直流电流表,需要________联一个阻值为________Ω的
电阻;
(2)能用所给微安表及一个电阻箱改装成一个量程为3V的电压表吗?如果能,如何改装?如果不能,
请说明理由。
_
(3)如果某同学先用所给器材组装一个量程为1mA的电流表,在此基础上再将它
改装成量程为3V的电压表。组装好的多用电表有电流量程1mA和电压量程
3V两挡。请你在右图虚线框内画出电路图并标出R1和R2,其中为公共接线

柱,a和b分别是电流挡和电压挡的接线柱。
答案:
(1) 并;100
(2) 不能;因为改装成3V电压表需串联分压电阻$ R=\frac{U - I_gR_g}{I_g}=\frac{3 - 100×10^{-6}×900}{100×10^{-6}}=29100\Omega $,而电阻箱最大阻值为9999.9Ω<29100Ω,故无法实现。
(3) 电路图如下:
(以公共接线柱*为起点,*与a之间并联微安表和R1;*与b之间为上述并联电路串联R2)
(说明:图中应画出公共端*,电流挡a:*接微安表与R1并联的两端;电压挡b:*接并联电路一端,并联电路另一端串联R2后接b)
(1) 并;100
(2) 不能;因为改装成3V电压表需串联分压电阻$ R=\frac{U - I_gR_g}{I_g}=\frac{3 - 100×10^{-6}×900}{100×10^{-6}}=29100\Omega $,而电阻箱最大阻值为9999.9Ω<29100Ω,故无法实现。
(3) 电路图如下:
(以公共接线柱*为起点,*与a之间并联微安表和R1;*与b之间为上述并联电路串联R2)
(说明:图中应画出公共端*,电流挡a:*接微安表与R1并联的两端;电压挡b:*接并联电路一端,并联电路另一端串联R2后接b)
59.(2025.陕西延安8月开学考)图甲为某物理兴趣小组组装完成的简易多用电表的
电路图。图中E是电池,R1、R2是定值电阻,R3是可调电阻,表头G的满偏电流为1mA,内阻为
180Ω。虚线方框内为换挡开关,A端和B端分别与两表笔相连。该多用电表有3个挡位,分别为:直
流电流10mA挡,直流电压2.5V挡,欧姆挡。
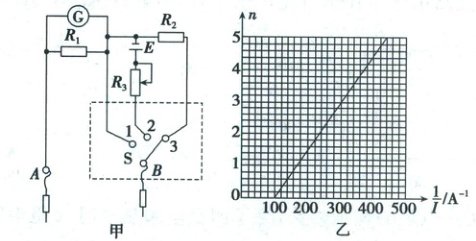
(1)图甲中的A端与(填“红”或“黑”)色表笔相连接;
(2)根据已知条件可求得电阻R1的阻值为Ω,电阻R2的阻值为Ω;
(3)经欧姆调零后,小明同学打算测量此欧姆表的内阻和电池的电动势,他找到5个规格相同的标准电
阻R=100.0Ω,他将n个(n=1,2,3,4,5)电阻串联后先后接在该欧姆表的红黑表笔之间,记下串联电
阻的个数n和对应的干路电流I。根据所得数据作出n−$\frac{1}{I}$图像,如图乙所示,可求得欧姆表中电池的
电动势为V,该欧姆表的内阻为Ω(结果均保留3位有效数字)。
电路图。图中E是电池,R1、R2是定值电阻,R3是可调电阻,表头G的满偏电流为1mA,内阻为
180Ω。虚线方框内为换挡开关,A端和B端分别与两表笔相连。该多用电表有3个挡位,分别为:直
流电流10mA挡,直流电压2.5V挡,欧姆挡。

(1)图甲中的A端与(填“红”或“黑”)色表笔相连接;
(2)根据已知条件可求得电阻R1的阻值为Ω,电阻R2的阻值为Ω;
(3)经欧姆调零后,小明同学打算测量此欧姆表的内阻和电池的电动势,他找到5个规格相同的标准电
阻R=100.0Ω,他将n个(n=1,2,3,4,5)电阻串联后先后接在该欧姆表的红黑表笔之间,记下串联电
阻的个数n和对应的干路电流I。根据所得数据作出n−$\frac{1}{I}$图像,如图乙所示,可求得欧姆表中电池的
电动势为V,该欧姆表的内阻为Ω(结果均保留3位有效数字)。
答案:
(1)红
(2)20;232
(3)1.25;125
解析:
(1) 多用电表中电流从红表笔流入,黑表笔流出,A端与表头串联,故A端接红色表笔。
(2) 求$R_1$(直流电流10mA挡):
表头满偏电流$I_g=1mA=0.001A$,内阻$r_g=180Ω$。10mA挡时表头与$R_1$并联,总电流$I=10mA=0.01A$。
并联电压相等:$I_g r_g=(I - I_g)R_1$,
代入数据:$0.001×180=(0.01 - 0.001)R_1$,解得$R_1=20Ω$。
求$R_2$(直流电压2.5V挡):
表头与$R_1$并联电阻$R_{并}=\frac{r_g R_1}{r_g + R_1}=\frac{180×20}{180 + 20}=18Ω$。
电压挡时总电流为10mA,由$U=I(R_{并}+R_2)$得:
$2.5=0.01×(18 + R_2)$,解得$R_2=232Ω$。
(3) 欧姆表原理与图像分析:
接入$n$个电阻时,总外电阻$R_{外}=100nΩ$,由闭合电路欧姆定律$E=I(R_{内}+100n)$,变形得$n=\frac{E}{100}·\frac{1}{I}-\frac{R_{内}}{100}$。
图像斜率$k=\frac{E}{100}$,纵轴截距$b=-\frac{R_{内}}{100}$。
由图乙,斜率$k=\frac{5 - 0}{500 - 100}=0.0125$,故$E=k×100=1.25V$。
截距$b=-1.25=-\frac{R_{内}}{100}$,解得$R_{内}=125Ω$。
(1)红
(2)20;232
(3)1.25;125
解析:
(1) 多用电表中电流从红表笔流入,黑表笔流出,A端与表头串联,故A端接红色表笔。
(2) 求$R_1$(直流电流10mA挡):
表头满偏电流$I_g=1mA=0.001A$,内阻$r_g=180Ω$。10mA挡时表头与$R_1$并联,总电流$I=10mA=0.01A$。
并联电压相等:$I_g r_g=(I - I_g)R_1$,
代入数据:$0.001×180=(0.01 - 0.001)R_1$,解得$R_1=20Ω$。
求$R_2$(直流电压2.5V挡):
表头与$R_1$并联电阻$R_{并}=\frac{r_g R_1}{r_g + R_1}=\frac{180×20}{180 + 20}=18Ω$。
电压挡时总电流为10mA,由$U=I(R_{并}+R_2)$得:
$2.5=0.01×(18 + R_2)$,解得$R_2=232Ω$。
(3) 欧姆表原理与图像分析:
接入$n$个电阻时,总外电阻$R_{外}=100nΩ$,由闭合电路欧姆定律$E=I(R_{内}+100n)$,变形得$n=\frac{E}{100}·\frac{1}{I}-\frac{R_{内}}{100}$。
图像斜率$k=\frac{E}{100}$,纵轴截距$b=-\frac{R_{内}}{100}$。
由图乙,斜率$k=\frac{5 - 0}{500 - 100}=0.0125$,故$E=k×100=1.25V$。
截距$b=-1.25=-\frac{R_{内}}{100}$,解得$R_{内}=125Ω$。
查看更多完整答案,请扫码查看


