《2026年一本密卷高考物理》

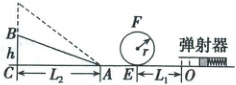
9. (2025·辽宁省抚顺市高三三模)如图所示，一弹射游戏装置由安装在水平台面上的固定弹射器、竖直圆轨道（在最低点$E$分别与水平轨道$EO$和$EA$相连）、高度$h$可调的斜轨道$AB$组成。游戏时滑块从$O$点弹出，经过圆轨道并滑上斜轨道。全程不脱离轨道且恰好停在$B$端则视为游戏成功。已知圆轨道半径$r = 0.1m$，$OE$长$L_{1}=0.2m$，$AC$长$L_{2}=0.4m$，圆轨道和$AE$光滑，滑块与$AB$、$OE$之间的动摩擦因数$\mu = 0.5$。滑块质量$m = 2g$且可视为质点，弹射时从静止释放且弹簧的弹性势能完全转化为滑块的动能。假设最大静摩擦力等于滑动摩擦力，忽略空气阻力，各部分平滑连接。求：
(1)滑块恰好能过圆轨道最高点$F$时的速度$v_{F}$的大小；
(2)当$h = 0.1m$且游戏成功时，滑块经过$E$点对圆轨道的压力$F_{N}$的大小及弹簧的弹性势能$E_{p0}$；
(3)要使游戏成功，弹簧的弹性势能$E_{p}$与高度$h$之间应满足的关系。

答案： 9.解析：
(1)滑块恰过$F$点的条件为$mg=m\frac{v_{F}^{2}}{r}$，解得$v_{F}=1m/s$；
(2)滑块在斜面上运动受重力、支持力和摩擦力，其中仅重力和摩擦力做功从$E$点到$B$点，根据动能定理有$-mgh-\mu mg\cos\theta x=-mgh-\mu mgL_{2}=0-\frac{1}{2}mv_{E}^{2}$代入数据解得$v_{E}=\sqrt{6}m/s$在$E$点，根据牛顿第二定律有$F_{N}'-mg=m\frac{v_{E}^{2}}{r}$，解得$F_{N}'=0.14N$由牛顿第三定律可知，滑块经过$E$点对圆轨道的压力$F_{N}=F_{N}'=0.14N$从$O$点到$E$点，根据能量守恒定律有$E_{p0}-\mu mgL_{1}=\frac{1}{2}mv_{E}^{2}$，解得$E_{p0}=8.0×10^{-3}J$；
(3)要使游戏成功，首先滑块不能脱离轨道，其次滑块需要恰好停留在$B$点，设滑块恰能过$F$点，从$O$点到$F$点，由能量守恒定律可得$E_{p1}=2mgr+\mu mgL_{1}+\frac{1}{2}mv_{F}^{2}=7.0×10^{-3}J$滑块恰能过$F$点且恰好能停留在$B$点，设此时$B$点离地高度为$h_{1}$，从$O$点到$B$点能量守恒有$E_{p1}-mgh_{1}-\mu mg(L_{1}+L_{2})=0$，解得$h_{1}=0.05m$由于滑块需要停留在$B$点，则需要$\mu mg\cos\theta\geq mg\sin\theta$，解得$\tan\theta\leq0.5$即$B$点离地高度最高为$h_{2}=L_{2}×0.5=0.2m$从$O$点到$B$点$E_{p}=mgh+\mu mg(L_{1}+L_{2})=2×10^{-3}(10h+3)J$，其中$0.05m\leq h\leq0.2m$。
答案：
(1)$1m/s$
(2)$0.14N$ $8.0×10^{-3}J$
(3)$E_{p}=2×10^{-3}(10h+3)J(0.05m\leq h\leq0.2m)$