《2026年一本密卷高考物理》

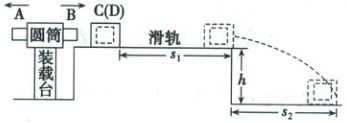
10. 如图，某爆炸能量测量装置由装载台和滑轨等构成，$C$是可以在滑轨上运动的标准测量件，其规格可以根据测量需求进行调整。滑轨安装在高度为$h$的水平面上。测量时，将弹药放入装载台圆筒内，两端用物块$A$和$B$封装，装载台与滑轨等高。引爆后，假设弹药释放的能量完全转化为$A$和$B$的动能。极短时间内$B$嵌入$C$中形成组合体$D$，$D$与滑轨间的动摩擦因数为$\mu$。$D$在滑轨上运动$s_1$距离后抛出，落地点距抛出点水平距离为$s_2$，根据$s_2$可计算出弹药释放的能量。某次测量中，$A$、$B$、$C$质量分别为$3m$、$1m$、$5m$，$s_1=\frac{h}{\mu}$，整个过程发生在同一竖直平面内，不计空气阻力，重力加速度大小为$g$。则(BD)


A.$D$的初动能与爆炸后瞬间$A$的动能相等
B.$D$的初动能与其落地时的动能相等
C.弹药释放的能量为$36mgh\left(1+\frac{s_2^2}{4h^2}\right)$
D.弹药释放的能量为$48mgh\left(1+\frac{s_2^2}{4h^2}\right)$

答案： 10.BD　A.爆炸过程，A与B组成的系统动量守恒，以向右为正方向，根据动量守恒定律得：$0 = - 3mv_A + mv_B$，B与C碰撞过程，同理可得：$mv_B = (m + 5m)v$，联立解得D的初速度大小为：$v = 0.5v_A$，爆炸后瞬间A的动能为：$E_{kA} = \frac{1}{2}·3mv_A^2$，D的初动能为：$E_{kD} = \frac{1}{2}·6m·(0.5v_A)^2 = \frac{3}{4}mv_A^2$，可见D的初动能与爆炸后瞬间A的动能不相等，故A错误;B、D水平滑动$s_1$距离的过程中摩擦力做功为：$W_f = - \mu·6mg· s_1 = - \mu·6mg·\frac{h}{\mu} = - 6mgh$，做平抛运动过程中重力做的功为：$W_G = 6mgh$，可得：$W_f + W_G = 0$，故D从开始运动到落地瞬间合外力做功为零，根据动能定理可知D的初动能与其落地时的动能相等，故B正确;CD、D平抛过程在竖直方向上有：$h = \frac{1}{2}gt^2$，在水平方向上有：$s_2 = v_0t$，联立可得：$v_0 = s_2\sqrt{\frac{g}{2h}}$。D水平滑动$s_1$距离的过程，根据动能定理有：$- 6mgh = \frac{1}{2}·6mv_0^2 - \frac{1}{2}·6mv^2$，解得：$v^2 = \frac{s_2^2g}{2h} + 2gh$，由A选项的解答可得：$v_A = 2v$，$v_B = 6v$，弹药释放的能量为：$E = \frac{1}{2}·3mv_A^2 + \frac{1}{2}mv_B^2 = 24mv^2 = 24m(\frac{s_2^2g}{2h} + 2gh) = 48mgh(1 + \frac{s_2^2}{4h^2})$，故C错误，D正确。

11. (7分)某同学通过观察小球在黏性液体中的运动，探究其动力学规律，步骤如下：
(1) 用螺旋测微器测量小球直径$D$如图1所示，$D=$2.205$mm$；
(2) 在液面处由静止释放小球，同时使用频闪摄影仪记录小球下落过程中不同时刻的位置，频闪仪每隔$0.5s$闪光一次。装置及所拍照片示意图如图2所示(图中的数字是小球到液面的测量距离，单位是$cm$)，根据照片分析，小球在$A$、$E$两点间近似做匀速运动，速度大小$v=$0.010$m/s$(保留2位有效数字)；
(3) 小球在液体中运动时受到液体的黏滞阻力$f=kDv$($k$为与液体有关的常量)，已知小球密度为$\rho$，液体密度为$\rho_0$，重力加速度大小为$g$，则$k$的表达式为$k=$$\frac{(\rho - \rho_0)g\pi D^2}{6v}$(用题中给出的物理量表示)；
(4) 为了进一步探究动力学规律，换成直径更小的同种材质小球，进行上述实验，匀速运动时的速度将减小(填“增大”“减小”或“不变”)。

答案： 11.解析：
(1)根据图1可知小球直径$D = 2mm + 20.5×0.01mm = 2.205mm$;
(2)由图2可知A、E两点间的距离为$x = (7.02 - 5.00)×10^{-2}m = 2.02×10^{-2}m$，时间为$t = 4t_0 = 4×0.5s = 2s$，所以速度为$v = \frac{x}{t} = \frac{2.02×10^{-2}m}{2s} \approx 0.010m/s$;
(3)小球匀速运动，根据受力平衡有$\rho gV = \rho_0gV + f$，求得体积公式为$V = \frac{4}{3}\pi R^3 = \frac{4}{3}\pi(\frac{D}{2})^3$，整理可得$k = \frac{(\rho - \rho_0)gV}{Dv} = \frac{(\rho - \rho_0)g\pi D^2}{6v}$;
(4)根据
(3)可知$v \propto D^2$，所以换成直径更小的同种材质小球，速度将减小。
答案：
(1)2.205　
(2)0.010　
(3)$\frac{(\rho - \rho_0)g\pi D^2}{6v}$　
(4)减小