《2026年南方凤凰台5A新考案数学二轮提高版》

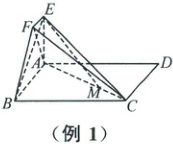
例1 如图，四边形$ABCD$为正方形，$EA \perp$平面$ABCD$，$EF // AB$，$AB = 4$，$AE = 2$，$EF = 1$.
(1) 求证：$BC \perp AF$；
(2) 若点$M$在线段$AC$上，且满足$CM = \frac{1}{4}CA$，求证：$EM //$平面$FBC$；
(3) 求证：$AF \perp$平面$EBC$.

答案：
例1　[解答]
(1)因为$EF// AB$，所以$EF$与$AB$确定平面$EABF$.因为$EA\perp$平面$ABCD,BC\subset$平面$ABCD$，所以$EA\perp BC$.由已知得$AB\perp BC$且$EA\cap AB = A,EA,AB\subset$平面$EABF$，所以$BC\perp$平面$EABF$.又$AF\subset$平面$EABF$，所以$BC\perp AF$.
(2)如图，过点$M$作$MN\perp BC$，垂足为$N$，连接$FN$，则$MN// AB$.又$CM=\frac{1}{4}AC$，所以$MN=\frac{1}{4}AB$.又$EF// AB$且$EF=\frac{1}{4}AB$，所以$EF// MN$且$EF = MN$，所以四边形$EFNM$为平行四边形，所以$EM// FN$.又$FN\subset$平面$FBC,EM\not\subset$平面$FBC$，所以$EM//$平面$FBC$.
(3)由
(1)可知，$AF\perp BC$.在四边形$ABFE$中，$AB = 4,AE = 2,EF = 1,\angle BAE=\angle AEF = 90^{\circ}$，所以$\tan\angle EBA=\tan\angle FAE=\frac{1}{2}$，则$\angle EBA=\angle FAE$.设$AF\cap BE = P$.因为$\angle PAE+\angle PAB = 90^{\circ}$，所以$\angle PBA+\angle PAB = 90^{\circ}$，则$\angle APB = 90^{\circ}$，即$EB\perp AF$.又$EB\cap BC = B,EB,BC\subset$平面$EBC$，所以$AF\perp$平面$EBC$.

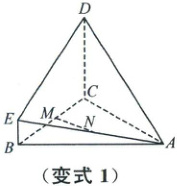
变式1 如图，在四棱锥$A - BCDE$中，$BE // CD$，$BE \perp BC$，$AB = AC$，平面$BCDE \perp$平面$ABC$，$M$为$BC$的中点.
(1) 若$N$是线段$AE$的中点，求证：$MN //$平面$ACD$；
(2) 若$BE = 1$，$BC = 2$，$CD = 3$，求证：$DE \perp$平面$AME$.

答案：
变式1　[解答]
(1)如图
(1)，取$AB$的中点$P$，连接$PM,PN$.因为$N,P$分别是$AE,AB$的中点，所以$NP// BE$，又因为$BE// CD$，所以$NP// CD$.又$NP\not\subset$平面$ACD,CD\subset$平面$ACD$，所以$NP//$平面$ACD$.同理，因为$M,P$分别是$BC,AB$的中点，所以$MP// AC$.又$MP\not\subset$平面$ACD,AC\subset$平面$ACD$，所以$MP//$平面$ACD$.又$MP\cap NP = P,MP,NP\subset$平面$MPN$，所以平面$MPN//$平面$ACD$.又$MN\subset$平面$MPN$，所以$MN//$平面$ACD$.

(2)如图
(2)，连接$AM,DM,EM$.由$AB = AC,M$为$BC$的中点，得$AM\perp BC$.又平面$BCDE\perp$平面$ABC$，平面$BCDE\cap$平面$ABC = BC,AM\subset$平面$ABC$，所以$AM\perp$平面$BCDE$.又$DE\subset$平面$BCDE$，所以$AM\perp DE$.在$Rt\triangle EBM$中，$BE = 1,BM=\frac{1}{2}BC = 1$，由勾股定理得$EM=\sqrt{2}$.在$Rt\triangle DCM$中，$CD = 3,CM=\frac{1}{2}BC = 1$，由勾股定理得$DM=\sqrt{10}$.在直角梯形$BCDE$中，由平面几何知识计算得$DE=\sqrt{(CD - BE)^2 + BC^2}=\sqrt{4 + 4}=2\sqrt{2}$，所以$EM^2 + DE^2 = DM^2$，所以$EM\perp DE$.又$AM\cap EM = M,AM,EM\subset$平面$AME$，所以$DE\perp$平面$AME$.