2026年南方凤凰台5A新考案数学二轮提高版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年南方凤凰台5A新考案数学二轮提高版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
变式 1 在$\triangle ABC$中,角$A$,$B$,$C$所对的边分别是$a$,$b$,$c$,且$a$不是最大边。若$a^{2} - b^{2} = 2bc\sin A$,则$\tan A - 9\tan B$的最小值是
-2
.
答案:
变式1 $-2$【解析】由余弦定理得$a^{2}-b^{2}=c^{2}-2bc\cos A$,则$c^{2}-2bc\cos A = 2bc\sin A$,即$c - 2b\cos A = 2b\sin A$,由正弦定理得$\sin C-2\cos A\sin B = 2\sin A\sin B$,则$\sin A\cos B-\cos A\sin B = 2\sin A\sin B$,所以$\tan A-\tan B = 2\tan A\tan B$,则$\frac{1}{\tan B}-\frac{1}{\tan A}=2$,即$\tan B=\frac{\tan A}{2\tan A + 1}$。
方法一:$\tan A-9\tan B=\tan A-\frac{9\tan A}{2\tan A + 1}=\frac{1}{2}(2\tan A + 1)+\frac{9}{2(2\tan A + 1)}-5\geqslant - 2$,当且仅当$\tan A = 1$时取等号。
方法二:$\tan A-9\tan B=\frac{1}{2}(\tan A-9\tan B)\left(\frac{1}{\tan B}-\frac{1}{\tan A}\right)=\frac{1}{2}\left(\frac{\tan A}{\tan B}+9\frac{\tan B}{\tan A}-10\right)\geqslant - 2$,当且仅当$\tan A = 1$时取等号。
方法一:$\tan A-9\tan B=\tan A-\frac{9\tan A}{2\tan A + 1}=\frac{1}{2}(2\tan A + 1)+\frac{9}{2(2\tan A + 1)}-5\geqslant - 2$,当且仅当$\tan A = 1$时取等号。
方法二:$\tan A-9\tan B=\frac{1}{2}(\tan A-9\tan B)\left(\frac{1}{\tan B}-\frac{1}{\tan A}\right)=\frac{1}{2}\left(\frac{\tan A}{\tan B}+9\frac{\tan B}{\tan A}-10\right)\geqslant - 2$,当且仅当$\tan A = 1$时取等号。
例 2 (1)在$\triangle ABC$中,角$A$,$B$,$C$的对边分别为$a$,$b$,$c$,$\triangle ABC$的面积为$S$。已知$a = 4$,$2S = a^{2} - (b - c)^{2}$,则$\triangle ABC$周长的最大值为
(2)(2025·长沙期末)在$\triangle ABC$中,角$A$,$B$,$C$所对的边分别为$a$,$b$,$c$,且外接圆半径为$R = 5$,则$\frac{abc}{a^{2} + b^{2} + 2c^{2}}$的最大值为
4 + 4\sqrt{5}
.(2)(2025·长沙期末)在$\triangle ABC$中,角$A$,$B$,$C$所对的边分别为$a$,$b$,$c$,且外接圆半径为$R = 5$,则$\frac{abc}{a^{2} + b^{2} + 2c^{2}}$的最大值为
\sqrt{5}
.
答案:
例2
(1)$4 + 4\sqrt{5}$ [解析]因为$2S=a^{2}-(b - c)^{2}$,而$S=\frac{1}{2}bc\sin A$,所以$2×\frac{1}{2}bc\sin A=a^{2}-(b - c)^{2}$,整理得$a^{2}=b^{2}+c^{2}-bc(2-\sin A)$。由余弦定理$a^{2}=b^{2}+c^{2}-2bc\cos A$,可得$2-\sin A = 2\cos A$。又因为$\sin^{2}A+\cos^{2}A = 1$,$A\in(0,\pi)$,所以$\sin A=\frac{4}{5}$,$\cos A=\frac{3}{5}$。又因为$a = 4$,所以由$a^{2}=b^{2}+c^{2}-bc(2-\sin A)$,可得$16=b^{2}+c^{2}-\frac{6}{5}bc=(b + c)^{2}-\frac{16}{5}bc\geqslant(b + c)^{2}-\frac{16}{5}\left(\frac{b + c}{2}\right)^{2}$,解得$b + c\leqslant4\sqrt{5}$,当且仅当$b = c = 2\sqrt{5}$时等号成立,所以$\triangle ABC$的周长$a + b + c\leqslant4 + 4\sqrt{5}$,即$\triangle ABC$周长的最大值为$4 + 4\sqrt{5}$。
(2)$\sqrt{5}$ [解析]方法一(正弦定理+余弦定理+基本不等式+三角最值):设$a^{2}+b^{2}+2c^{2}=t$,由余弦定理可得$a^{2}+b^{2}-c^{2}=2ab\cos C$,所以$2a^{2}+2b^{2}-2c^{2}=4ab\cos C$,所以$3(a^{2}+b^{2})=t + 4ab\cos C$。因为$a^{2}+b^{2}\geqslant2ab$,所以$t + 4ab\cos C\geqslant6ab$,即$ab\leqslant\frac{t}{6 - 4\cos C}$,当且仅当$a = b$时取等号。因为外接圆半径为$R = 5$,所以$c = 2R\sin C = 10\sin C$。因为$C\in(0,\pi)$,所以$\frac{C}{2}\in\left(0,\frac{\pi}{2}\right)$,所以$\tan\frac{C}{2}>0$,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}=\frac{abc}{t}\leqslant\frac{c}{6 - 4\cos C}=\frac{10\sin C}{6 - 4\cos C}=\frac{5\sin C}{3 - 2\cos C}$。令$\frac{5\sin C}{3 - 2\cos C}=k$,则$5\sin C+2k\cos C = 3k$,即$3k=\sqrt{25 + 4k^{2}}\sin(C+\varphi)$,则$3|k|\leqslant\sqrt{25 + 4k^{2}}$,所以$5k^{2}\leqslant25$,所以$k\leqslant\sqrt{5}$,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}$的最大值为$\sqrt{5}$。
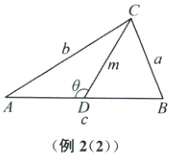
方法二(正弦定理+中线长定理+基本不等式+面积法):如图,取$AB$的中点$D$,连接$CD$,设$CD = m$。由$S=\frac{1}{2}ab\sin C=\frac{abc}{4R}$,及$2(a^{2}+b^{2})=c^{2}+(2m)^{2}$(平行四边形对角线的平方和等于四条边的平方和),得原式$=\frac{20S}{a^{2}+b^{2}+2c^{2}}=\frac{20S}{\frac{5}{2}c^{2}+2m^{2}}\leqslant\frac{20S}{2\sqrt{5}cm}=\frac{20×\frac{1}{2}cmsin\theta}{2\sqrt{5}cm}=\sqrt{5}\sin\theta\leqslant\sqrt{5}$,当且仅当$\theta=\frac{\pi}{2}$且$c^{2}=\frac{4}{5}m^{2}$,即$a = b$且$c^{2}=\frac{4}{5}m^{2}$时取等号,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}$的最大值为$\sqrt{5}$。
方法三(正弦定理+加权形式的外森比克不等式):由$S=\frac{1}{2}ab\sin C=\frac{abc}{4R}$,得$\frac{abc}{a^{2}+b^{2}+2c^{2}}=\frac{20S}{a^{2}+b^{2}+2c^{2}}$。由加权形式的外森比克不等式,得$a^{2}+b^{2}+2c^{2}\geqslant4\sqrt{1 + 2 + 2}S = 4\sqrt{5}S$,所以原式$=\frac{20S}{a^{2}+b^{2}+2c^{2}}\leqslant\frac{20S}{4\sqrt{5}S}=\sqrt{5}$,当且仅当$\cot A:\cot B:\cot C = 1:1:2$时取等号,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}$的最大值为$\sqrt{5}$。
例2
(1)$4 + 4\sqrt{5}$ [解析]因为$2S=a^{2}-(b - c)^{2}$,而$S=\frac{1}{2}bc\sin A$,所以$2×\frac{1}{2}bc\sin A=a^{2}-(b - c)^{2}$,整理得$a^{2}=b^{2}+c^{2}-bc(2-\sin A)$。由余弦定理$a^{2}=b^{2}+c^{2}-2bc\cos A$,可得$2-\sin A = 2\cos A$。又因为$\sin^{2}A+\cos^{2}A = 1$,$A\in(0,\pi)$,所以$\sin A=\frac{4}{5}$,$\cos A=\frac{3}{5}$。又因为$a = 4$,所以由$a^{2}=b^{2}+c^{2}-bc(2-\sin A)$,可得$16=b^{2}+c^{2}-\frac{6}{5}bc=(b + c)^{2}-\frac{16}{5}bc\geqslant(b + c)^{2}-\frac{16}{5}\left(\frac{b + c}{2}\right)^{2}$,解得$b + c\leqslant4\sqrt{5}$,当且仅当$b = c = 2\sqrt{5}$时等号成立,所以$\triangle ABC$的周长$a + b + c\leqslant4 + 4\sqrt{5}$,即$\triangle ABC$周长的最大值为$4 + 4\sqrt{5}$。
(2)$\sqrt{5}$ [解析]方法一(正弦定理+余弦定理+基本不等式+三角最值):设$a^{2}+b^{2}+2c^{2}=t$,由余弦定理可得$a^{2}+b^{2}-c^{2}=2ab\cos C$,所以$2a^{2}+2b^{2}-2c^{2}=4ab\cos C$,所以$3(a^{2}+b^{2})=t + 4ab\cos C$。因为$a^{2}+b^{2}\geqslant2ab$,所以$t + 4ab\cos C\geqslant6ab$,即$ab\leqslant\frac{t}{6 - 4\cos C}$,当且仅当$a = b$时取等号。因为外接圆半径为$R = 5$,所以$c = 2R\sin C = 10\sin C$。因为$C\in(0,\pi)$,所以$\frac{C}{2}\in\left(0,\frac{\pi}{2}\right)$,所以$\tan\frac{C}{2}>0$,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}=\frac{abc}{t}\leqslant\frac{c}{6 - 4\cos C}=\frac{10\sin C}{6 - 4\cos C}=\frac{5\sin C}{3 - 2\cos C}$。令$\frac{5\sin C}{3 - 2\cos C}=k$,则$5\sin C+2k\cos C = 3k$,即$3k=\sqrt{25 + 4k^{2}}\sin(C+\varphi)$,则$3|k|\leqslant\sqrt{25 + 4k^{2}}$,所以$5k^{2}\leqslant25$,所以$k\leqslant\sqrt{5}$,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}$的最大值为$\sqrt{5}$。
方法二(正弦定理+中线长定理+基本不等式+面积法):如图,取$AB$的中点$D$,连接$CD$,设$CD = m$。由$S=\frac{1}{2}ab\sin C=\frac{abc}{4R}$,及$2(a^{2}+b^{2})=c^{2}+(2m)^{2}$(平行四边形对角线的平方和等于四条边的平方和),得原式$=\frac{20S}{a^{2}+b^{2}+2c^{2}}=\frac{20S}{\frac{5}{2}c^{2}+2m^{2}}\leqslant\frac{20S}{2\sqrt{5}cm}=\frac{20×\frac{1}{2}cmsin\theta}{2\sqrt{5}cm}=\sqrt{5}\sin\theta\leqslant\sqrt{5}$,当且仅当$\theta=\frac{\pi}{2}$且$c^{2}=\frac{4}{5}m^{2}$,即$a = b$且$c^{2}=\frac{4}{5}m^{2}$时取等号,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}$的最大值为$\sqrt{5}$。

方法三(正弦定理+加权形式的外森比克不等式):由$S=\frac{1}{2}ab\sin C=\frac{abc}{4R}$,得$\frac{abc}{a^{2}+b^{2}+2c^{2}}=\frac{20S}{a^{2}+b^{2}+2c^{2}}$。由加权形式的外森比克不等式,得$a^{2}+b^{2}+2c^{2}\geqslant4\sqrt{1 + 2 + 2}S = 4\sqrt{5}S$,所以原式$=\frac{20S}{a^{2}+b^{2}+2c^{2}}\leqslant\frac{20S}{4\sqrt{5}S}=\sqrt{5}$,当且仅当$\cot A:\cot B:\cot C = 1:1:2$时取等号,所以$\frac{abc}{a^{2}+b^{2}+2c^{2}}$的最大值为$\sqrt{5}$。
变式 2 (1)在$\triangle ABC$中,$a$,$b$,$c$分别是角$A$,$B$,$C$的三边长,若$a^{2} + b^{2} + 2c^{2} = 8$,则$\triangle ABC$面积的最大值为
(2)在锐角三角形$ABC$中,$a$,$b$,$c$分别是角$A$,$B$,$C$的对边,若$b\cos C + \frac{1}{2}c = a$,$c = 1$,则$a^{2} + b^{2}$的取值范围为
\frac{2\sqrt{5}}{5}
.(2)在锐角三角形$ABC$中,$a$,$b$,$c$分别是角$A$,$B$,$C$的对边,若$b\cos C + \frac{1}{2}c = a$,$c = 1$,则$a^{2} + b^{2}$的取值范围为
(1,7)
.
答案:
变式2
(1)$\frac{2\sqrt{5}}{5}$ 方法一(余弦定理+基本不等式+三角最值):由$a^{2}+b^{2}+2c^{2}=8$,得$a^{2}+b^{2}+2(a^{2}+b^{2}-2ab\cos C)=8$,即$3(a^{2}+b^{2})=8 + 4ab\cos C$,又$a^{2}+b^{2}\geqslant2ab$,所以$8 + 4ab\cos C\geqslant6ab$,所以$ab\leqslant\frac{4}{3 - 2\cos C}$,所以$S_{\triangle ABC}=\frac{1}{2}ab\sin C\leqslant\frac{2\sin C}{3 - 2\cos C}$。令$\frac{2\sin C}{3 - 2\cos C}=t$,则$2\sin C+2t\cos C = 3t$,即$|3t|\leqslant2\sqrt{t^{2}+1}$,所以$5t^{2}\leqslant4$,所以$t$的最大值为$\frac{2\sqrt{5}}{5}$。
方法二(三斜求积+整体代换+基本不等式):由$a^{2}+b^{2}+2c^{2}=8$,得$a^{2}+b^{2}=8 - 2c^{2}$,所以$S_{\triangle ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}ab\sqrt{1-\left(\frac{a^{2}+b^{2}-c^{2}}{2ab}\right)^{2}}=\frac{1}{2}\sqrt{a^{2}b^{2}-\left(\frac{a^{2}+b^{2}-c^{2}}{2}\right)^{2}}\leqslant\frac{1}{2}\sqrt{\left(\frac{a^{2}+b^{2}}{2}\right)^{2}-\left(\frac{4 - c^{2}}{2}\right)^{2}}=\frac{1}{2}\sqrt{c^{2}(4 - c^{2})}\leqslant\frac{1}{2}×2×\frac{2\sqrt{5}}{5}=\frac{2\sqrt{5}}{5}$,当且仅当$a^{2}=b^{2}$且$c^{2}=\frac{8}{5}$,$a^{2}=b^{2}=\frac{12}{5}$时取等号。
方法三(中线长定理+基本不等式):由$2(a^{2}+b^{2})=c^{2}+(2m)^{2}$(平行四边形对角线的平方和等于四条边的平方和),得$a^{2}+b^{2}=\frac{1}{2}c^{2}+2m^{2}=8 - 2c^{2}$,所以$m^{2}+\frac{5}{4}c^{2}=4\geqslant2\sqrt{\frac{5}{4}}mc=\sqrt{5}mc$,所以$mc$的最大值为$\frac{4\sqrt{5}}{5}$,则$S=\frac{1}{2}mc\sin\theta\leqslant\frac{1}{2}mc\leqslant\frac{2\sqrt{5}}{5}$。

方法四(加权形式的外森比克不等式):$a^{2}+b^{2}+2c^{2}=8\geqslant4\sqrt{1 + 2 + 2}S = 4\sqrt{5}S$,当且仅当$\cot A:\cot B:\cot C = 1:1:2$时取等号,所以$S\leqslant\frac{2\sqrt{5}}{5}$。
(2)$(1,7)$ [解析]因为$b\cos C+\frac{1}{2}c = a$,所以由正弦定理得$2\sin B\cos C+\sin C = 2\sin A = 2\sin(B + C)=2\sin B\cos C+2\cos B\sin C$,整理得$2\cos B\sin C=\sin C$,因为$B,C\in(0,\pi)$,所以$\sin C>0$,所以$\cos B=\frac{1}{2}$,所以$B=\frac{\pi}{3}$。因为$\triangle ABC$为锐角三角形,所以$\begin{cases}0<C<\frac{\pi}{2}\\0<\frac{2\pi}{3}-C<\frac{\pi}{2}\end{cases}$,解得$C\in\left(\frac{\pi}{6},\frac{\pi}{2}\right)$。又因为$B=\frac{\pi}{3}$,$c = 1$,所以由正弦定理$\frac{a}{\sin A}=\frac{c}{\sin C}$,得$a=\frac{c\sin A}{\sin C}$,同理$b=\frac{c\sin B}{\sin C}=\frac{\frac{\sqrt{3}}{2}}{\sin C}$,所以$a^{2}+b^{2}=\frac{\sin^{2}A}{\sin^{2}C}+\frac{3}{4\sin^{2}C}=\frac{4\sin^{2}A + 3}{4\sin^{2}C}=\frac{4\sin^{2}\left(\frac{2\pi}{3}-C\right)+3}{4\sin^{2}C}=\frac{3\cos^{2}C+\sin^{2}C+2\sqrt{3}\sin C\cos C+3}{4\sin^{2}C}=\frac{6\cos^{2}C+4\sin^{2}C+2\sqrt{3}\sin C\cos C+3}{4\sin^{2}C}=\frac{3}{2\tan^{2}C}+\frac{\sqrt{3}}{2\tan C}+1$,因为$C\in\left(\frac{\pi}{6},\frac{\pi}{2}\right)$,所以$\tan C>\frac{\sqrt{3}}{3}$,令$t=\frac{1}{\tan C}\in(0,\sqrt{3})$,所以$a^{2}+b^{2}=\frac{3}{2}t^{2}+\frac{\sqrt{3}}{2}t + 1$在$t\in(0,\sqrt{3})$上单调递增,则$1 < a^{2}+b^{2}<7$,所以$a^{2}+b^{2}$的取值范围为$(1,7)$。
变式2
(1)$\frac{2\sqrt{5}}{5}$ 方法一(余弦定理+基本不等式+三角最值):由$a^{2}+b^{2}+2c^{2}=8$,得$a^{2}+b^{2}+2(a^{2}+b^{2}-2ab\cos C)=8$,即$3(a^{2}+b^{2})=8 + 4ab\cos C$,又$a^{2}+b^{2}\geqslant2ab$,所以$8 + 4ab\cos C\geqslant6ab$,所以$ab\leqslant\frac{4}{3 - 2\cos C}$,所以$S_{\triangle ABC}=\frac{1}{2}ab\sin C\leqslant\frac{2\sin C}{3 - 2\cos C}$。令$\frac{2\sin C}{3 - 2\cos C}=t$,则$2\sin C+2t\cos C = 3t$,即$|3t|\leqslant2\sqrt{t^{2}+1}$,所以$5t^{2}\leqslant4$,所以$t$的最大值为$\frac{2\sqrt{5}}{5}$。
方法二(三斜求积+整体代换+基本不等式):由$a^{2}+b^{2}+2c^{2}=8$,得$a^{2}+b^{2}=8 - 2c^{2}$,所以$S_{\triangle ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}ab\sqrt{1-\left(\frac{a^{2}+b^{2}-c^{2}}{2ab}\right)^{2}}=\frac{1}{2}\sqrt{a^{2}b^{2}-\left(\frac{a^{2}+b^{2}-c^{2}}{2}\right)^{2}}\leqslant\frac{1}{2}\sqrt{\left(\frac{a^{2}+b^{2}}{2}\right)^{2}-\left(\frac{4 - c^{2}}{2}\right)^{2}}=\frac{1}{2}\sqrt{c^{2}(4 - c^{2})}\leqslant\frac{1}{2}×2×\frac{2\sqrt{5}}{5}=\frac{2\sqrt{5}}{5}$,当且仅当$a^{2}=b^{2}$且$c^{2}=\frac{8}{5}$,$a^{2}=b^{2}=\frac{12}{5}$时取等号。
方法三(中线长定理+基本不等式):由$2(a^{2}+b^{2})=c^{2}+(2m)^{2}$(平行四边形对角线的平方和等于四条边的平方和),得$a^{2}+b^{2}=\frac{1}{2}c^{2}+2m^{2}=8 - 2c^{2}$,所以$m^{2}+\frac{5}{4}c^{2}=4\geqslant2\sqrt{\frac{5}{4}}mc=\sqrt{5}mc$,所以$mc$的最大值为$\frac{4\sqrt{5}}{5}$,则$S=\frac{1}{2}mc\sin\theta\leqslant\frac{1}{2}mc\leqslant\frac{2\sqrt{5}}{5}$。

方法四(加权形式的外森比克不等式):$a^{2}+b^{2}+2c^{2}=8\geqslant4\sqrt{1 + 2 + 2}S = 4\sqrt{5}S$,当且仅当$\cot A:\cot B:\cot C = 1:1:2$时取等号,所以$S\leqslant\frac{2\sqrt{5}}{5}$。
(2)$(1,7)$ [解析]因为$b\cos C+\frac{1}{2}c = a$,所以由正弦定理得$2\sin B\cos C+\sin C = 2\sin A = 2\sin(B + C)=2\sin B\cos C+2\cos B\sin C$,整理得$2\cos B\sin C=\sin C$,因为$B,C\in(0,\pi)$,所以$\sin C>0$,所以$\cos B=\frac{1}{2}$,所以$B=\frac{\pi}{3}$。因为$\triangle ABC$为锐角三角形,所以$\begin{cases}0<C<\frac{\pi}{2}\\0<\frac{2\pi}{3}-C<\frac{\pi}{2}\end{cases}$,解得$C\in\left(\frac{\pi}{6},\frac{\pi}{2}\right)$。又因为$B=\frac{\pi}{3}$,$c = 1$,所以由正弦定理$\frac{a}{\sin A}=\frac{c}{\sin C}$,得$a=\frac{c\sin A}{\sin C}$,同理$b=\frac{c\sin B}{\sin C}=\frac{\frac{\sqrt{3}}{2}}{\sin C}$,所以$a^{2}+b^{2}=\frac{\sin^{2}A}{\sin^{2}C}+\frac{3}{4\sin^{2}C}=\frac{4\sin^{2}A + 3}{4\sin^{2}C}=\frac{4\sin^{2}\left(\frac{2\pi}{3}-C\right)+3}{4\sin^{2}C}=\frac{3\cos^{2}C+\sin^{2}C+2\sqrt{3}\sin C\cos C+3}{4\sin^{2}C}=\frac{6\cos^{2}C+4\sin^{2}C+2\sqrt{3}\sin C\cos C+3}{4\sin^{2}C}=\frac{3}{2\tan^{2}C}+\frac{\sqrt{3}}{2\tan C}+1$,因为$C\in\left(\frac{\pi}{6},\frac{\pi}{2}\right)$,所以$\tan C>\frac{\sqrt{3}}{3}$,令$t=\frac{1}{\tan C}\in(0,\sqrt{3})$,所以$a^{2}+b^{2}=\frac{3}{2}t^{2}+\frac{\sqrt{3}}{2}t + 1$在$t\in(0,\sqrt{3})$上单调递增,则$1 < a^{2}+b^{2}<7$,所以$a^{2}+b^{2}$的取值范围为$(1,7)$。
例 3 (1)满足$AB = 2$,$AC = \sqrt{2}BC$的$\triangle ABC$的面积的最大值是
(2)(2025·芜湖二模)(多选)在$\triangle ABC$中,已知$CA + CB = 10$,$AB = 8$,则此三角形的面积可能为(
A. $e^{2}$
B. $10\sqrt{3}$
C. $12$
D. $15$
2\sqrt{2}
.(2)(2025·芜湖二模)(多选)在$\triangle ABC$中,已知$CA + CB = 10$,$AB = 8$,则此三角形的面积可能为(
AC
)A. $e^{2}$
B. $10\sqrt{3}$
C. $12$
D. $15$
答案:
例3
(1)$2\sqrt{2}$ [解析]
(1)方法一:设$BC = x$,则$AC=\sqrt{2}x$,根据面积公式得$S_{\triangle ABC}=\frac{1}{2}AB· BC\sin B=\frac{1}{2}×2x\sqrt{1-\cos^{2}B}$,由余弦定理得$\cos B=\frac{AB^{2}+BC^{2}-AC^{2}}{2AB· BC}=\frac{4 + x^{2}-(\sqrt{2}x)^{2}}{4x}=\frac{4 - x^{2}}{4x}$,代入上式得$S_{\triangle ABC}=x\sqrt{1-\left(\frac{4 - x^{2}}{4x}\right)^{2}}=\sqrt{\frac{128-(x^{2}-12)^{2}}{16}}$,由三角形三边关系得$\begin{cases}\sqrt{2}x+x>2\\2+x>\sqrt{2}x\end{cases}$,解得$2\sqrt{2}-2<x<2\sqrt{2}+2$,故当$x = 2\sqrt{3}$时,$S_{\triangle ABC}$取得最大值$2\sqrt{2}$。
方法二:以$AB$的中垂线为$y$轴建立平面直角坐标系(图略),则$A(-1,0)$,$B(1,0)$,设$C(x,y)(y\neq0)$,则$(x + 1)^{2}+y^{2}=2(x - 1)^{2}+2y^{2}$,化简得$x^{2}+y^{2}-6x + 1 = 0(y\neq0)$,即$(x - 3)^{2}+y^{2}=8(y\neq0)$,圆周上的点到$x$轴的距离的最大值为$2\sqrt{2}$,所以$(S_{\triangle ABC})_{\max}=\frac{1}{2}×2×2\sqrt{2}=2\sqrt{2}$。
(2)$AC$【解析】方法一:记$\triangle ABC$内角$A$,$B$,$C$的对边分别为$a$,$b$,$c$。因为$CA + CB = 10$,$AB = 8$,即$a + b = 10$,$c = 8$,所以$\cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}=\frac{(a + b)^{2}-2ab - c^{2}}{2ab}=\frac{10^{2}-2ab - 8^{2}}{2ab}=\frac{18}{ab}-1$。因为$0 < C<\pi$,所以$\sin C=\sqrt{1-\cos^{2}C}=\sqrt{1-\left(\frac{18}{ab}-1\right)^{2}}=6\sqrt{\frac{1}{ab}-\frac{9}{(ab)^{2}}}$,故$\triangle ABC$的面积$S=\frac{1}{2}ab\sin C=\frac{1}{2}ab×6\sqrt{\frac{1}{ab}-\frac{9}{(ab)^{2}}}=3\sqrt{ab - 9}$。因为$ab\leqslant\left(\frac{a + b}{2}\right)^{2}=25$,当且仅当$a = b = 5$时等号成立,所以$S = 3\sqrt{ab - 9}\leqslant3×\sqrt{25 - 9}=12$,则此三角形面积的最大值为$12$。因为$10\sqrt{3}>12$,$15>12$,$e^{2}<12$,所以$A$,$C$正确。
方法二:以$AB$的中垂线为$y$轴,建立平面直角坐标系(图略),点$C$在椭圆$\frac{x^{2}}{25}+\frac{y^{2}}{9}=1(y\neq0)$上,可知当点$C$为椭圆的上、下顶点时,$\triangle ABC$的面积最大,为$\frac{1}{2}×8×3 = 12$,所以$S_{\triangle ABC}\in(0,12]$。
(1)$2\sqrt{2}$ [解析]
(1)方法一:设$BC = x$,则$AC=\sqrt{2}x$,根据面积公式得$S_{\triangle ABC}=\frac{1}{2}AB· BC\sin B=\frac{1}{2}×2x\sqrt{1-\cos^{2}B}$,由余弦定理得$\cos B=\frac{AB^{2}+BC^{2}-AC^{2}}{2AB· BC}=\frac{4 + x^{2}-(\sqrt{2}x)^{2}}{4x}=\frac{4 - x^{2}}{4x}$,代入上式得$S_{\triangle ABC}=x\sqrt{1-\left(\frac{4 - x^{2}}{4x}\right)^{2}}=\sqrt{\frac{128-(x^{2}-12)^{2}}{16}}$,由三角形三边关系得$\begin{cases}\sqrt{2}x+x>2\\2+x>\sqrt{2}x\end{cases}$,解得$2\sqrt{2}-2<x<2\sqrt{2}+2$,故当$x = 2\sqrt{3}$时,$S_{\triangle ABC}$取得最大值$2\sqrt{2}$。
方法二:以$AB$的中垂线为$y$轴建立平面直角坐标系(图略),则$A(-1,0)$,$B(1,0)$,设$C(x,y)(y\neq0)$,则$(x + 1)^{2}+y^{2}=2(x - 1)^{2}+2y^{2}$,化简得$x^{2}+y^{2}-6x + 1 = 0(y\neq0)$,即$(x - 3)^{2}+y^{2}=8(y\neq0)$,圆周上的点到$x$轴的距离的最大值为$2\sqrt{2}$,所以$(S_{\triangle ABC})_{\max}=\frac{1}{2}×2×2\sqrt{2}=2\sqrt{2}$。
(2)$AC$【解析】方法一:记$\triangle ABC$内角$A$,$B$,$C$的对边分别为$a$,$b$,$c$。因为$CA + CB = 10$,$AB = 8$,即$a + b = 10$,$c = 8$,所以$\cos C=\frac{a^{2}+b^{2}-c^{2}}{2ab}=\frac{(a + b)^{2}-2ab - c^{2}}{2ab}=\frac{10^{2}-2ab - 8^{2}}{2ab}=\frac{18}{ab}-1$。因为$0 < C<\pi$,所以$\sin C=\sqrt{1-\cos^{2}C}=\sqrt{1-\left(\frac{18}{ab}-1\right)^{2}}=6\sqrt{\frac{1}{ab}-\frac{9}{(ab)^{2}}}$,故$\triangle ABC$的面积$S=\frac{1}{2}ab\sin C=\frac{1}{2}ab×6\sqrt{\frac{1}{ab}-\frac{9}{(ab)^{2}}}=3\sqrt{ab - 9}$。因为$ab\leqslant\left(\frac{a + b}{2}\right)^{2}=25$,当且仅当$a = b = 5$时等号成立,所以$S = 3\sqrt{ab - 9}\leqslant3×\sqrt{25 - 9}=12$,则此三角形面积的最大值为$12$。因为$10\sqrt{3}>12$,$15>12$,$e^{2}<12$,所以$A$,$C$正确。
方法二:以$AB$的中垂线为$y$轴,建立平面直角坐标系(图略),点$C$在椭圆$\frac{x^{2}}{25}+\frac{y^{2}}{9}=1(y\neq0)$上,可知当点$C$为椭圆的上、下顶点时,$\triangle ABC$的面积最大,为$\frac{1}{2}×8×3 = 12$,所以$S_{\triangle ABC}\in(0,12]$。
变式 3 在$\triangle ABC$中,角$A$,$B$,$C$所对的边分别为$a$,$b$,$c$,若$BC = a = 6$,$\sin B = \frac{1}{2}\sin C$,则当$\triangle ABC$的面积最大时,$AC$的长为
2\sqrt{5}
.
答案:
变式3 $2\sqrt{5}$【解析】因为$\sin B=\frac{1}{2}\sin C$,由正弦定理可得$b=\frac{1}{2}c$,即$c = 2b$。因为$BC = 6$,不妨令$B(-3,0)$,$C(3,0)$,设点$A$的坐标为$(x,y)(y\neq0)$,则点$A$的轨迹方程满足$\sqrt{(x + 3)^{2}+y^{2}}=2\sqrt{(x - 3)^{2}+y^{2}}$,整理可得$(x - 5)^{2}+y^{2}=16(y\neq0)$,即点$A$的轨迹是以$(5,0)$为圆心,$4$为半径的圆(与$x$轴的两交点除外),当点$A$的坐标$A(5,4)$或$A(5,-4)$时,$\triangle ABC$的面积最大,其最大值为$S=\frac{1}{2}×6×4 = 12$,此时$AC=\sqrt{(5 - 3)^{2}+(4 - 0)^{2}}=2\sqrt{5}$。
查看更多完整答案,请扫码查看


