《2026年南方凤凰台5A新考案数学二轮提高版》

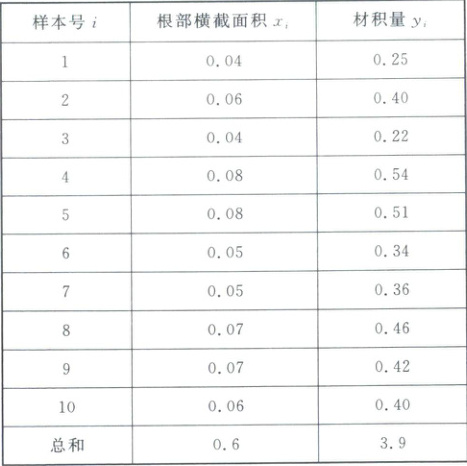
变式 2 （$2022$·全国乙卷）某地经过多年的环境治理，已将荒山改造成了绿水青山。为估计一林区某种树木的总材积量，随机选取了$10$棵这种树木，测量每棵树的根部横截面积（单位：$m^{2}$）和材积量（单位：$m^{3}$），得到如下数据：
并计算得$\sum_{i = 1}^{10}x_{i}^{2}=0.038$，$\sum_{i = 1}^{10}y_{i}^{2}=1.6158$，$\sum_{i = 1}^{10}x_{i}y_{i}=0.2474$。
（1）估计该林区这种树木平均一棵的根部横截面积与平均一棵的材积量。
（2）求该林区这种树木的根部横截面积与材积量的样本相关系数（精确到$0.01$）。
（3）现测量了该林区所有这种树木的根部横截面积，并得到所有这种树木的根部横截面积总和为$186m^{2}$。已知树木的材积量与其根部横截面积近似成正比。利用以上数据给出该林区这种树木的总材积量的估计值。（参考数据：$\sqrt{1.896}\approx1.377$）平均一棵的根部横截面积为0.06m²，平均一棵的材积量为0.39m³；样本相关系数约为0.97；总材积量的估计值为1209m³

答案： 变式2 【解答】
(1)估计该林区这种树木平均一棵的根部横截面积$\overline{x} = \frac{\sum_{i = 1}^{10}x_{i}}{10} = \frac{0.6}{10} = 0.06(m^{2})$，估计该林区这种树木平均一棵的材积量$\overline{y} = \frac{\sum_{i = 1}^{10}y_{i}}{10} = \frac{3.9}{10} = 0.39(m^{3})$.
(2)$\sum_{i = 1}^{10}(x_{i} - \overline{x})(y_{i} - \overline{y}) = \sum_{i = 1}^{10}x_{i}y_{i} - 10\overline{x}\overline{y} = 0.0134$，$\sum_{i = 1}^{10}(x_{i} - \overline{x})^{2} = \sum_{i = 1}^{10}x_{i}^{2} - 10\overline{x}^{2} = 0.002$，$\sum_{i = 1}^{10}(y_{i} - \overline{y})^{2} = \sum_{i = 1}^{10}y_{i}^{2} - 10\overline{y}^{2} = 0.0948$，所以$\sqrt{\sum_{i = 1}^{10}(x_{i} - \overline{x})^{2}\sum_{i = 1}^{10}(y_{i} - \overline{y})^{2}} = \sqrt{0.002 × 0.0948} = \sqrt{0.0001896} \approx 0.01 × 1.377 =0.01377$，所以样本相关系数$r = \frac{\sum_{i = 1}^{10}(x_{i} - \overline{x})(y_{i} - \overline{y})}{\sqrt{\sum_{i = 1}^{10}(x_{i} - \overline{x})^{2}\sum_{i = 1}^{10}(y_{i} - \overline{y})^{2}}} \approx \frac{0.0134}{0.01377} \approx 0.97$.
(3)设该林区这种树木的总材积量的估计值为$Y m^{3}$，由题意可知，该种树木的材积量与其根部横截面积近似成正比，所以$\frac{3.9}{0.6} = \frac{Y}{186}$，所以$Y = \frac{186 × 3.9}{0.6} = 1209$，即该林区这种树木的总材积量的估计值为$1209 m^{3}$.