第67页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
24. (12分)如图①,已知点C在线段AB上,线段AC= 10cm,BC= 6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC= a,其他条件不变,求MN的长度;
(3)如图②,动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿BA向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
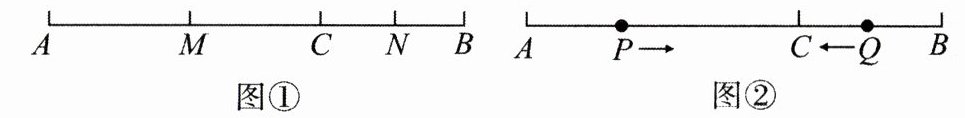
(1)求线段MN的长度;
(2)根据第(1)题的计算过程和结果,设AC+BC= a,其他条件不变,求MN的长度;
(3)如图②,动点P、Q分别从A、B同时出发,点P以2cm/s的速度沿AB向右运动,终点为B,点Q以1cm/s的速度沿BA向左运动,终点为A,当一个点到达终点,另一个点也随之停止运动,求运动多少秒时,C、P、Q三点有一点恰好是以另两点为端点的线段的中点?
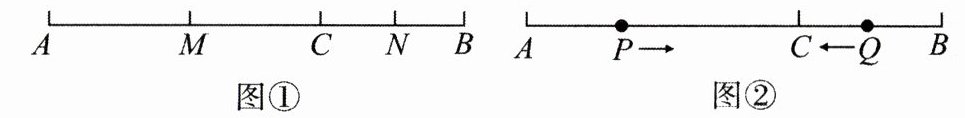
答案:
(1)
∵线段AC = 10 cm,BC = 6 cm,点M、N分别是AC、BC的中点,
∴CM = $\frac{1}{2}$AC = 5 cm,CN = $\frac{1}{2}$BC = 3 cm,
∴MN = CM + CN = 8 cm;
(2)
∵点M、N分别是AC、BC的中点,
∴CM = $\frac{1}{2}$AC,CN = $\frac{1}{2}$BC,
∴MN = CM + CN = $\frac{1}{2}$AC + $\frac{1}{2}$BC = $\frac{1}{2}$a;
(3)①当0 < t ≤ 5时,C是线段PQ的中点,得10 - 2t = 6 - t,解得t = 4;②当5 < t ≤ $\frac{16}{3}$时,P为线段CQ的中点,2t - 10 = 16 - 3t,解得t = $\frac{26}{5}$;③当$\frac{16}{3}$ < t ≤ 6时,Q为线段PC的中点,6 - t = 3t - 16,解得t = $\frac{11}{2}$;④当6 < t ≤ 8时,C为线段PQ的中点,2t - 10 = t - 6,解得t = 4(舍去)。综上所述,t = 4或$\frac{26}{5}$或$\frac{11}{2}$。
(1)
∵线段AC = 10 cm,BC = 6 cm,点M、N分别是AC、BC的中点,
∴CM = $\frac{1}{2}$AC = 5 cm,CN = $\frac{1}{2}$BC = 3 cm,
∴MN = CM + CN = 8 cm;
(2)
∵点M、N分别是AC、BC的中点,
∴CM = $\frac{1}{2}$AC,CN = $\frac{1}{2}$BC,
∴MN = CM + CN = $\frac{1}{2}$AC + $\frac{1}{2}$BC = $\frac{1}{2}$a;
(3)①当0 < t ≤ 5时,C是线段PQ的中点,得10 - 2t = 6 - t,解得t = 4;②当5 < t ≤ $\frac{16}{3}$时,P为线段CQ的中点,2t - 10 = 16 - 3t,解得t = $\frac{26}{5}$;③当$\frac{16}{3}$ < t ≤ 6时,Q为线段PC的中点,6 - t = 3t - 16,解得t = $\frac{11}{2}$;④当6 < t ≤ 8时,C为线段PQ的中点,2t - 10 = t - 6,解得t = 4(舍去)。综上所述,t = 4或$\frac{26}{5}$或$\frac{11}{2}$。
查看更多完整答案,请扫码查看


