第61页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
24. (12 分)在数轴上,图中点 $A$ 表示 $-36$,点 $B$ 表示 $44$,动点 $P、Q$ 分别从 $A、B$ 两点同时出发,相向而行,动点 $P、Q$ 的运动速度之比是 $3:2$(速度单位:$1$ 个单位长度/秒)。$12$ 秒后,动点 $P$ 到达原点 $O$,动点 $Q$ 到达点 $C$,设运动的时间为 $t(t > 0)$ 秒。
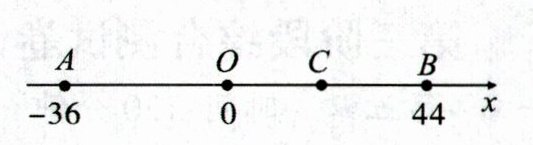
(1)求 $OC$ 的长;
(2)经过 $t$ 秒,$P、Q$ 两点之间相距 $5$ 个单位长度,求 $t$ 的值;
(3)若动点 $P$ 到达 $B$ 点后,以原速度立即返回,当 $P$ 点运动至原点时,动点 $Q$ 是否到达点 $A$?若到达,求提前到达了多少时间;若未能到达,说明理由。
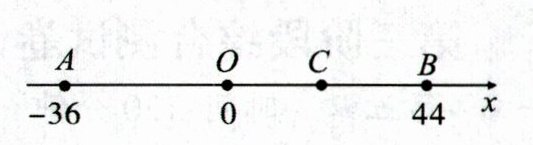
(1)求 $OC$ 的长;
(2)经过 $t$ 秒,$P、Q$ 两点之间相距 $5$ 个单位长度,求 $t$ 的值;
(3)若动点 $P$ 到达 $B$ 点后,以原速度立即返回,当 $P$ 点运动至原点时,动点 $Q$ 是否到达点 $A$?若到达,求提前到达了多少时间;若未能到达,说明理由。
答案:
(1)设P、Q速度分别为3m个单位长度/秒,2m个单位长度/秒,12×3m=36,所以m=1.所以P、Q速度分别为3个单位长度/秒,2个单位长度/秒.所以BC=12×2=24.所以OC=OB-BC=44-24=20;
(2)当A、B在相遇前且相距5个单位长度时,3t+2t+5=44+36,5t=75,所以t=15.当A、B在相遇后且相距5个单位长度时,3t+2t-5=44+36,5t=85,所以t=17.综上所述,t的值为15或17;
(3)P运动到原点时,$t=\frac{36+44+44}{3}=\frac{124}{3}$(s),此时QB=$2×\frac{124}{3}=\frac{248}{3}>44+36=80$.所以Q点已到达点A.所以Q点已到达点A的时间为$\frac{36+44}{2}=40$(秒).故提前的时间为$\frac{124}{3}-40=\frac{4}{3}$(秒).
(1)设P、Q速度分别为3m个单位长度/秒,2m个单位长度/秒,12×3m=36,所以m=1.所以P、Q速度分别为3个单位长度/秒,2个单位长度/秒.所以BC=12×2=24.所以OC=OB-BC=44-24=20;
(2)当A、B在相遇前且相距5个单位长度时,3t+2t+5=44+36,5t=75,所以t=15.当A、B在相遇后且相距5个单位长度时,3t+2t-5=44+36,5t=85,所以t=17.综上所述,t的值为15或17;
(3)P运动到原点时,$t=\frac{36+44+44}{3}=\frac{124}{3}$(s),此时QB=$2×\frac{124}{3}=\frac{248}{3}>44+36=80$.所以Q点已到达点A.所以Q点已到达点A的时间为$\frac{36+44}{2}=40$(秒).故提前的时间为$\frac{124}{3}-40=\frac{4}{3}$(秒).
查看更多完整答案,请扫码查看


