第39页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
10. 已知有理数 $a$、$b$、$c$ 在数轴上的位置如图,化简 $|a| - |a + b| + |c - a| + |b - c|$ 的值为 (
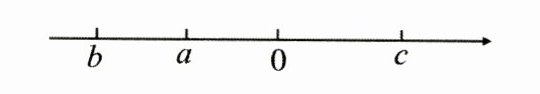
A.$2a - 2b$
B.$2c - a$
C.$a$
D.$-a$
B
)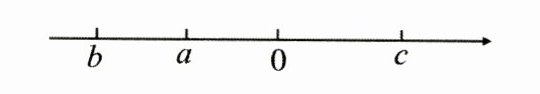
A.$2a - 2b$
B.$2c - a$
C.$a$
D.$-a$
答案:
B 【解析】由图知,b<a<0<c,|b|>|a|,|c|>|a|,所以|a|=-a,|a+b|=-(a+b),|c-a|=c-a,|b-c|=-(b-c),原式=-a+(a+b)+c-a-(b-c)=2c-a.
11. 已知 $a - b = 2$,则代数式 $2a - 2b - 3$ 的值是
1
.
答案:
1
12. 计算: $(-81) ÷ 2\frac{1}{4} × \frac{4}{9} ÷$
$1\frac{1}{15}$
$= -15$.
答案:
$1\frac{1}{15}$
13. 多项式 $8x^{2} - 3x + 5$ 与 $3x^{3} + 2mx^{2} - 5x + 7$ 相加后,不含 $x$ 的二次项,则常数 $m$ 的值为
-4
.
答案:
-4
14. 已知 $|a - 1| = 3$, $|b| = 3$, $a$、$b$ 在数轴上对应的点分别为 $A$、$B$.
(1) $A$、$B$ 两点间距离的最大值等于
(2) $A$、$B$ 两点间距离的最小值于
(1) $A$、$B$ 两点间距离的最大值等于
7
;(2) $A$、$B$ 两点间距离的最小值于
1
.
答案:
(1)7
(2)1
(1)7
(2)1
15. $1 \sim 9$ 这九个数字的乘方所得的结果,其个位数是有规律的,如: $2^{1} = 2$, $2^{2} = 4$, $2^{3} = 8$, $2^{4} = 16$, $2^{5} = 32$, $2^{6} = 64$, …$$ 由此知道 $2^{n}$ ($n$ 是正整数) 的个位数字按 $2$, $4$, $8$, $6$, $2$, $4$, $8$, $6…$ 的规律变化,其他数字的乘方也有类似的规律,根据这样的规律可知, $63^{2025}$ 的个位数字是
3
.
答案:
3【解析】类似$2^{n}$的个位数的规律,$63^{n}$的个位数字按3,9,7,1,3,9,7,1…循环,2025÷4=506……1,所以$63^{2025}$的个位数字是3,9,7,1的第一个,即3.
16. (6 分) 画一数轴,并把 $-4$, $-(-3.5)$, $2\frac{1}{2}$, $0$, $|-\frac{3}{2}|$ 各数在数轴上表示出来,再用“$<$”号把它们连接起来.
答案:
画数轴表示数略.用“<”号把它们连接起来-4<0<$|-\frac{3}{2}|<2\frac{1}{2}<-(-3.5)$.
查看更多完整答案,请扫码查看


