《2025年金榜名卷必刷卷七年级数学上册人教版》

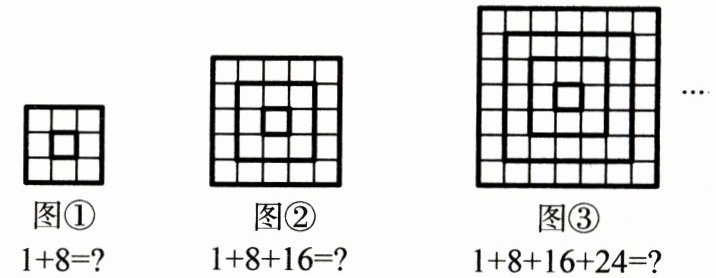
10.观察下列图形及图形所对应的算式,根据你发现的规律计算$1 + 8 + 16 + 24+…+8n(n$是正整数)的结果为 (A)
$1+8= ?$
$1+8+16= ?$
$1+8+16+24= ?$

A.$(2n + 1)^{2}$
B.$(2n - 1)^{2}$
C.$(n + 2)^{2}$
D.$n^{2}$

答案： A 【解析】图①1+8=9=3²,图②1+8+16=25=5²,图③1+8+16+24=49=7²,…它们都是连续奇数的平方,奇数一般用2n-1或2n+1表示,图①是3²=(2×1+1)²…,所以结果为(2n+1)².

11.多项式$5x-4xy^{2}+3$的项分别是5x,-4xy²,3.

答案： 5x,-4xy²,3

12.若单项式$2a^{x + 2}b^{2}与-3ab^{y}$的和仍是一个单项式,则$x^{y}= $1.

答案： 1

13.化简$(2xy - y)-2(-y + xy)= $y.

答案： y

14.有一组单项式:$a^{2},-\frac{a^{3}}{2},\frac{a^{4}}{3},-\frac{a^{5}}{4},…$,观察它们构成的规律,用你发现的规律写出:
(1)第10个单项式为$-\frac{a^{11}}{10}$;
(2)第$n$个单项式为$\frac{(-a)^{n+1}}{n}$.

答案： $(1)-\frac{a^{11}}{10};(2)\frac{(-a)^{n+1}}{n}$

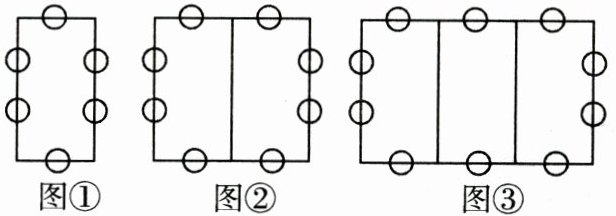
15.一张长方形桌子需配6把椅子,按如图方式将桌子拼在一起,那么8张桌子需配20把椅子.

答案： 20 【解析】观察发现每增加一张桌子,只增加上、下共2把椅子,图①6;图②6+2;图③6+2×2;图④6+2×3...n张桌子配椅子6+2(n-1).当n=8时,6+2(n-1)=20.

16.(6分)把下列各式填在相应的大括号里.
$0,x^{2},-x^{2}-2x + 5,\frac{9}{4},xy,8+\frac{b}{7},-5,\frac{x + y}{5}$.
(1)单项式:…$\{\}$;
(2)多项式:…$\{\}$;
(3)整式:…$\{\}$.

答案： $(1)0,x²,\frac{9}{4},xy,-5;(2)-x²-2x+5,8+\frac{b}{7},\frac{x+y}{5};(3)0,x²,-x²-2x+5,\frac{9}{4},xy,8+\frac{b}{7},-5,\frac{x+y}{5}$

17.(6分)合并同类项:
(1)$3x^{2}-1-2x-5 + 3x-x^{2}$;
(2)$\frac{2}{3}a^{2}-\frac{1}{2}ab+\frac{3}{4}a^{2}+ab-b^{2}$.

答案：
(1)原式=(3-1)x²+(-2+3)x+(-1-5)=2x²+x-6;
(2)原式$=(\frac{2}{3}+\frac{3}{4})a²+(-\frac{1}{2}+1)ab-b²=\frac{17}{12}a²+\frac{1}{2}ab-b².$