《2025年金榜名卷必刷卷七年级数学上册人教版》

19. (8分)有理数$a$、$b$、$c$在数轴上对应的位置如图所示.

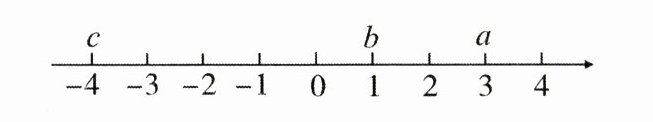
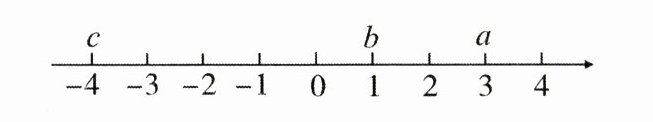
(1)在数轴上分别标出$a$、$b$、$c$的相反数所在的位置；
(2)比较$-a$、$-b$、$-c$的大小.

答案：
(1)a、b、c的相反数分别为-3,-1,4,画图略；
(2)-a＜-b＜-c.

20. (8分)已知$x+3= 0$,$|y+5|+4= 4$,数轴上$z对应的点到-2对应的点的距离是7$.求$x$、$y$、$z$这三个数两两之积的和.

答案： 因为x+3= 0,所以x=-3;因为|y+5|+4= 4,所以|y+5|=0.所以y=-5;因为z对应的点到-2对应的点的距离是7.所以z=5或z=-9.所以当z=5时,xy+yz+xz=(-3)×(-5)+(-5)×5+(-3)×5=-25;当z=-9时,xy+yz+xz=(-3)×(-5)+(-5)×(-9)+(-3)×(-9)=87.即x、y、z这三个数两两之积的和为-25或87.

21. (8分)计算$6÷(-\frac{1}{2}+\frac{1}{3})$时,李明同学的计算过程如下：
解：原式$=6÷(-\frac{1}{2})+6÷\frac{1}{3}= -12+18= 6$.
请你判断李明的计算过程是否正确,若不正确,请你写出正确的计算过程,并用正确方法计算$(\frac{1}{2}-\frac{1}{6}+\frac{1}{9})÷(-\frac{1}{36})+36÷(\frac{1}{2}-\frac{1}{6}+\frac{1}{9})$的值.

答案： 不正确.正确的计算过程:$6÷(-\frac{1}{2}+\frac{1}{3})=6÷(-\frac{1}{6})=-36$.原式=$(\frac{1}{2}-\frac{1}{6}+\frac{1}{9})÷(-\frac{1}{36})+36÷(\frac{1}{2}-\frac{1}{6}+\frac{1}{9})=-36×\frac{1}{2}+36×\frac{1}{6}-36×\frac{1}{9}+36×\frac{18}{8}=-18+6-4+36×\frac{9}{4}=-16+81=65$.