《2025年金榜名卷必刷卷七年级数学上册人教版》

9. 已知线段AB= 5,C是直线AB上一点,BC= 2,则线段AC长为(C)
A.7
B.3
C.3或7
D.以上都不对

答案： C

10. 某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在(A)

A.A区
B.B区
C.C区
D.A、B两区之间

答案： A

11. 已知一个长方体的长、宽、高分别是7cm、5cm、3cm,那么这个长方体的棱长和为60cm.

答案： 60

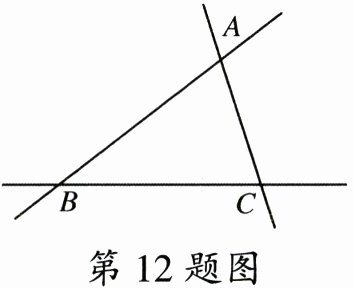
12. 直线AB、BC、CA的位置关系如图,则下列语句:①点A在直线BC上;②直线AB经过点C;③直线AB、BC、CA两两相交;④点B是直线AB、BC、CA的公共点,正确的为③.(填序号)

答案： ③

13. 四边形ABCD中,AB= 8,AD= 6,BC= 7.5,CD= 10,AC= 11,BD= 13,在四边形ABCD内找一点O,使它到四边形四个顶点的距离之和最小,则其最小和为24.

答案： 24

14. 如图是一个几何体的表面展开图.
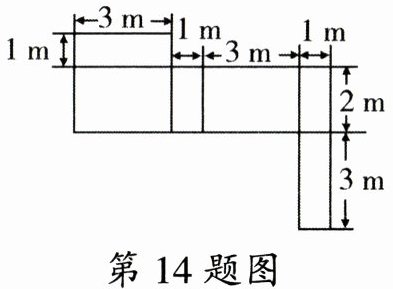
(1)该几何体是长方体;
(2)依据图中数据该几何体的体积为6$m^3.$

答案：
(1)长方体　
(2)6

15. 已知线段AC,点D为AC的中点,B是直线AC上的一点,且BC= $\frac{1}{2}$AB,BD= 1cm,则AC= 6cm或$\frac{2}{3}$cm.

答案： 6cm或$\frac{2}{3}$cm

16. (6分)(1)试一试在括号里写出下面这些基本图形的名称;

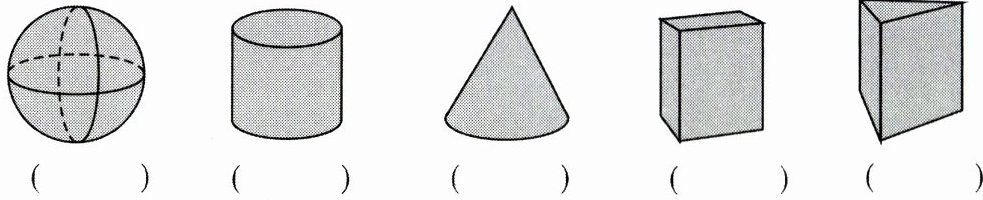
(2)将这些几何体分类,并写出分类的理由.
(1)从左向右依次是:球、圆柱、圆锥、长方体、三棱柱；
(2)观察图形，按柱、锥、球划分，则有圆柱、长方体、三棱柱为柱体；圆锥为锥体；球为球体。

答案：
(1)从左向右依次是:球、圆柱、圆锥、长方体、三棱柱；
(2)观察图形，按柱、锥、球划分，则有圆柱、长方体、三棱柱为柱体；圆锥为锥体；球为球体。