《2025年学习质量监测七年级数学上册人教版》

1. 若单项式$\frac{1}{2}x^{a + 1}y^2与-3x^{2a - 5}y^2$是同类项,则有(A).
A.$a + 1 = 2a - 5$
B.$(a + 1)+(2a - 5)= 0$
C.$a + 1 = 2$
D.$2a - 5 = 2$

答案： A

2. (2024,福建)今年我国国民经济开局良好,市场销售稳定增长,社会消费增长较快,第一季度社会消费品零售总额为$120327$亿元,比去年第一季度增长$4.7\%$,求去年第一季度社会消费品零售总额.若将去年第一季度社会消费品零售总额设为$x$亿元,则符合题意的方程是(A).
A.$(1 + 4.7\%)x = 120327$
B.$(1 - 4.7\%)x = 120327$
C.$\frac{x}{1 + 4.7\%}= 120327$
D.$\frac{x}{1 - 4.7\%}= 120327$

答案： A 【提示】利用今年第一季度社会消费品零售总额=去年第一季度社会消费品零售总额×(1+4.7%),即可列出关于x的方程,此题得解.

3. 一个长方形的周长为$26$ cm,若这个长方形的长减少$2$ cm,宽增加$1$ cm,就可成为一个正方形,设长方形的长为$x$ cm,根据题意,列出方程为x-2=13-x+1.

答案： x-2=13-x+1

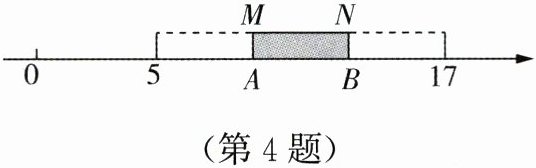
4. 如图,有一根木棒$MN$放置在数轴上,它的两端$M$,$N分别落在点A$,$B$处.将木棒在数轴上水平移动,当$M移动到点B$时,$N所对应的数为17$,当$N移动到点A$时,$M所对应的数为5$,求木棒$MN$的长.设木棒$MN的长为x$,列出方程为3x=17-5.

答案： 3x=17-5 【提示】由题意可知,5与17之间的长度等于3倍的木棒MN的长.

5. 根据问题,设未知数并列出方程.
《九章算术》是我国古代数学最重要的著作,奠定了我国古代数学的基本框架.《九章算术》中有这样一个问题：今有善行者行一百步,不善行者行六十步.今不善行者先行一百步,善行者追之,问几何步及之？译文：相同时间内,走路快的人走$100$步,走路慢的人只走$60$步.若走路慢的人先走$100$步,走路快的人要走多少步才能追上？(注：步为长度单位)

答案： 【解】设走路快的人要走x步才能追上,则x=100+$\frac{60}{100}$x.