第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. 某市出租车收费标准:路程不超过 $3$ km,收费 $9$ 元;超过 $3$ km 后,每 $1$ km 收费 $1.7$ 元. 如果某出租车行驶 $x$ km($x>3$,且 $x$ 为整数),那么应收费(
A.$(9 + 1.7x)$元
B.$(9 - 1.7x)$元
C.$[9 + 1.7(x - 3)]$元
D.$[9 - 1.7(x - 3)]$元
C
).A.$(9 + 1.7x)$元
B.$(9 - 1.7x)$元
C.$[9 + 1.7(x - 3)]$元
D.$[9 - 1.7(x - 3)]$元
答案:
C
2. 已知多项式 $-7a^{m}b^{n}+5ab^{2}-1$($m$,$n$ 为正整数)是按 $a$ 的降幂排列的四次三项式,则 $(-n)^{m}$ 的值为(
A.-1
B.3 或 - 4
C.-1 或 4
D.-3 或 4
C
).A.-1
B.3 或 - 4
C.-1 或 4
D.-3 或 4
答案:
C
3. 按一定规律排列的多项式:$a + 2b$,$a^{2}-4b^{2}$,$a^{3}+8b^{3}$,$a^{4}-16b^{4}$,…,则第 8 个多项式是
$a^{8}-2^{8}b^{8}$
.
答案:
$a^{8}-2^{8}b^{8}$
4. 已知式子 $M= (a + 2)x^{3}+(2b - 1)x^{2}-2x + 5$ 是关于 $x$ 的二次多项式,且二次项系数为 5,如图,数轴上 $A$,$B$ 两点所对应的数分别是 $a$ 和 $b$.

(1)$a=$
(2)$A$,$B$ 两点之间的距离为

(1)$a=$
-2
,$b=$3
;(2)$A$,$B$ 两点之间的距离为
5
.
答案:
(1)-2,3
(2)5
(1)-2,3
(2)5
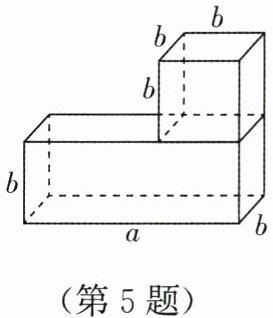
5. (1)如图,几何体是由一个长方体与一个正方体组成的,用整式表示这个几何体的体积,并指出它的次数.
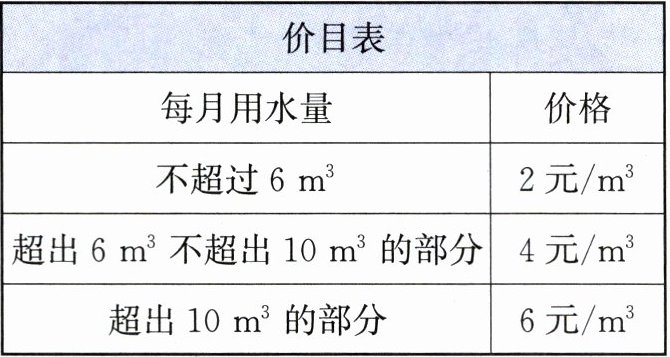
(2)(2023,部分区期中)为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段以达到节水的目的,该市自来水收费的价目表如下(消费按月份结算):
|价目表| |
|每月用水量|价格|
|不超过 $6m^{3}$| $2$ 元$/m^{3}$|
|超出 $6m^{3}$ 不超出 $10m^{3}$ 的部分| $4$ 元$/m^{3}$|
|超出 $10m^{3}$ 的部分| $6$ 元$/m^{3}$|
①某户居民 1 月份和 2 月份的用水量分别为 $5m^{3}$ 和 $8m^{3}$,则应收水费分别是______元和______元.

$ab^{2}+b^{3}$,它的次数为3.
(2)(2023,部分区期中)为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段以达到节水的目的,该市自来水收费的价目表如下(消费按月份结算):
|价目表| |
|每月用水量|价格|
|不超过 $6m^{3}$| $2$ 元$/m^{3}$|
|超出 $6m^{3}$ 不超出 $10m^{3}$ 的部分| $4$ 元$/m^{3}$|
|超出 $10m^{3}$ 的部分| $6$ 元$/m^{3}$|

①某户居民 1 月份和 2 月份的用水量分别为 $5m^{3}$ 和 $8m^{3}$,则应收水费分别是______元和______元.
10
20
②若该户居民 3 月份用水量为 $a m^{3}$(其中 $6 < a\leqslant10$),则应收水费多少元(用含 $a$ 的式子表示,并化简)?$6×2+(a-6)×4=(4a-12)$元.
③若该户居民 4 月份交水费 40 元,该户居民 4 月份用水多少立方米?如果用$6\ m^3$,水费为12元;如果用$10\ m^3$,水费为28元;所以4月份用水量超过$10\ m^3$.由题意得$\frac{40-28}{6}=2(m^3)$,$2+10=12(m^3)$,所以该户居民4月份用水$12\ m^3$.
答案:
【解】
(1)$ab^{2}+b^{3}$,它的次数为3.
(2)①10,20②$6×2+(a-6)×4=(4a-12)$元.③如果用$6\ m^3$,水费为12元;如果用$10\ m^3$,水费为28元;所以4月份用水量超过$10\ m^3$.由题意得$\frac{40-28}{6}=2(m^3)$,$2+10=12(m^3)$,所以该户居民4月份用水$12\ m^3$.
(1)$ab^{2}+b^{3}$,它的次数为3.
(2)①10,20②$6×2+(a-6)×4=(4a-12)$元.③如果用$6\ m^3$,水费为12元;如果用$10\ m^3$,水费为28元;所以4月份用水量超过$10\ m^3$.由题意得$\frac{40-28}{6}=2(m^3)$,$2+10=12(m^3)$,所以该户居民4月份用水$12\ m^3$.
查看更多完整答案,请扫码查看


