《2025年暑假作业八年级数学沪科版黄山书社》

6. 如下左图，在四边形 $ABCD$ 中，$AD = BC$，$AB = CD$，$AC$ 与 $BD$ 相交于点 $O$，请添加一个条件______，使四边形 $ABCD$ 是菱形。

答案： 6.答案不唯一,如AC⊥BD

7. 如上右图，在平面直角坐标系中，矩形 $OABC$ 的顶点 $A$，$C$ 的坐标分别为 $(10,0)$，$(0,4)$，点 $D$ 是 $OA$ 的中点，点 $P$ 在 $BC$ 上运动，当 $\triangle ODP$ 是腰长为 $5$ 的等腰三角形时，点 $P$ 的坐标为______。

答案： 7.(2,4)或(3,4)或(8,4)

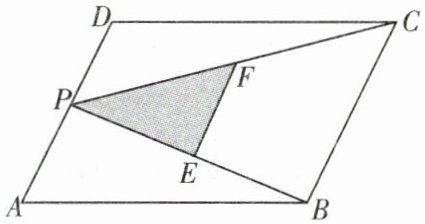
8. 如下左图，$P$ 为平行四边形 $ABCD$ 的边 $AD$ 上一点，点 $E$，$F$ 分别为 $PB$，$PC$ 的中点，$\triangle PEF$，$\triangle PDC$，$\triangle PAB$ 的面积分别为 $S$，$S_1$，$S_2$，若 $S = 2$，则 $S_1 + S_2=$______。

答案： 8.8

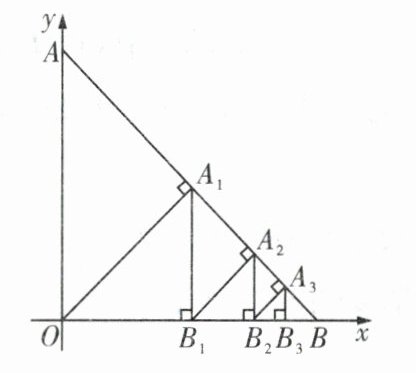
9. 如上右图，在平面直角坐标系中，点 $A$ 在 $y$ 轴上，点 $B$ 在 $x$ 轴上，$OA = OB = 4$。连接 $AB$，过点 $O$ 作 $OA_1\perp AB$ 于点 $A_1$，过点 $A_1$ 作 $A_1B_1\perp x$ 轴于点 $B_1$；过点 $B_1$ 作 $B_1A_2\perp AB$ 于点 $A_2$，过点 $A_2$ 作 $A_2B_2\perp x$ 轴于点 $B_2$；过点 $B_2$ 作 $B_2A_3\perp AB$ 于点 $A_3$，过点 $A_3$ 作 $A_3B_3\perp x$ 轴于点 $B_3$；……；按照如此规律操作下去，则点 $A_{2024}$ 的坐标为______。

答案： 9.(4 - $\frac{1}{2^{2022}}$, $\frac{1}{2^{2022}}$)

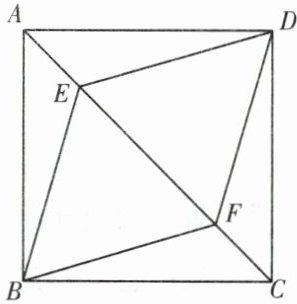
10. 如图，在正方形 $ABCD$ 中，点 $E$，$F$ 在 $AC$ 上，且 $AF = CE$。求证：四边形 $BEDF$ 是菱形。

答案：
∵四边形ABCD是正方形，
∴AB = AD = CD = BC，∠DAE = ∠BAE = ∠BCF = ∠DCF = 45°。在△ABE和△ADE中，$\begin{cases} AB = AD, \\ \angle BAE = \angle DAE, \\ AE = AE, \end{cases}$
∴△ABE ≌ △ADE(SAS)，
∴BE = DE。同理可得△BFC ≌ △DFC，
∴BF = DF。
∵AF = CE，
∴AF - EF = CE - EF，即AE = CF。在△ABE和△CBF中，$\begin{cases} AB = CB, \\ \angle BAE = \angle BCF, \\ AE = CF, \end{cases}$
∴△ABE ≌ △CBF(SAS)，
∴BE = BF，
∴BE = BF = DE = DF，
∴四边形BEDF是菱形。