《2025年暑假作业八年级数学沪科版黄山书社》

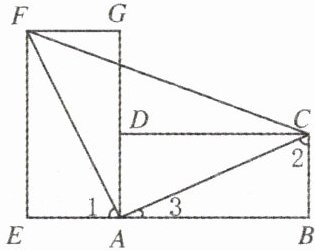
11. 如图,把两个形状和大小完全相同的矩形拼成如图所示的“L”形,连接AF,AC,CF,试判断△AFC的形状,并说明理由.

答案： $ \because $ 矩形 $ ABCD $ 与矩形 $ AGFE $ 的形状和大小完全一样, $ \therefore AE = BC $, $ EF = AB $, $ \angle E = \angle B = 90^\circ $, $ \therefore \triangle AEF \cong \triangle CBA $, $ \therefore AF = CA $, $ \angle 1 = \angle 2 $. $ \because \angle B = 90^\circ $, $ \therefore \angle 2 + \angle 3 = 90^\circ $, $ \therefore \angle 1 + \angle 3 = 90^\circ $, $ \therefore \angle FAC = 90^\circ $, $ \triangle AFC $ 是等腰直角三角形.

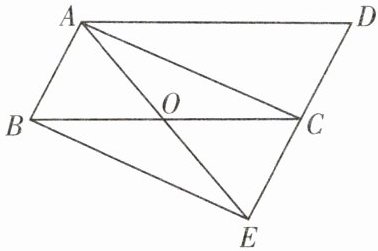
12. 如图,延长平行四边形ABCD的边DC至点E,使DC=CE.连接AE,AE与BC交于点O.
(1) 当∠EAD满足什么条件时,四边形ABEC为菱形?
(2) 求证:当∠AOC=2∠D时,四边形ABEC为矩形.

答案：
(1) 当 $ \angle EAD = 90^\circ $ 时, 四边形 $ ABEC $ 为菱形. 理由如下: $ \because $ 四边形 $ ABCD $ 是平行四边形, $ \therefore AB // CD $, $ AD // BC $, $ AB = CD $, $ \because DC = CE $, $ \therefore AB = CE $, $ \therefore $ 四边形 $ ABEC $ 是平行四边形. $ \because AD // BC $, $ \therefore \angle EOC = \angle EAD = 90^\circ $, $ \therefore AE \perp BC $, $ \therefore $ 平行四边形 $ ABEC $ 为菱形.
(2) 证明: $ \because $ 四边形 $ ABCD $ 是平行四边形, $ \therefore BC // AD $, $ \angle BCE = \angle D $. 由
(1) 可知, 四边形 $ ABEC $ 是平行四边形, $ \therefore OA = OE $, $ OB = OC $. $ \because \angle AOC = \angle OEC + \angle BCE $, $ \angle AOC = 2 \angle D $, $ \therefore \angle OEC = \angle D $, $ \therefore AE = AD $, $ \therefore AE = BC $, $ \therefore $ 平行四边形 $ ABEC $ 是矩形.

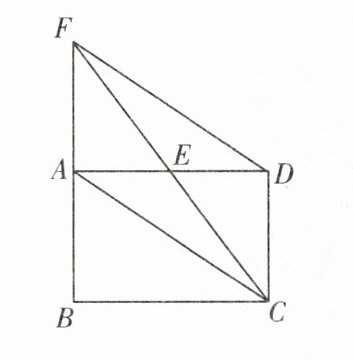
13. 如图,在矩形ABCD中,E是AD的中点,延长CE与BA,两延长线交于点F,连接AC,DF.
(1) 求证:四边形ACDF是平行四边形;
(2) 当CF平分∠BCD时,写出BC与CD的数量关系,并说明理由.

答案： 提示:
(1) 利用矩形的性质, 可判定 $ \triangle FAE \cong \triangle CDE $, 从而得到 $ CD = FA $. 再根据 $ CD // AF $, 即可得出四边形 $ ACDF $ 是平行四边形.
(2) $ \because CF $ 平分 $ \angle BCD $, $ \therefore \angle DCE = \angle BCE = 45^\circ $, $ \therefore \triangle CDE $ 是等腰直角三角形, $ \therefore CD = DE $. 又点 $ E $ 是 $ AD $ 的中点, $ \therefore AD = 2 DE = 2 CD $. $ \because AD = BC $, $ \therefore BC = 2 CD $.