《2025年暑假作业八年级数学沪科版黄山书社》

7. 如下左图，在 $\square ABCD$ 中，$AB = 10$，$AD = 6$，$AC \perp BC$，则 $BD =$ ______.

答案： 4$\sqrt{13}$

8. 如下中图，在正六边形 $ABCDEF$ 中，$M$，$N$ 是对角线 $BE$ 上的两点.添加下列条件中的一个：① $BM = EN$；② $\angle FAN = \angle CDM$；③ $AM = DN$；④ $\angle AMB = \angle DNE$.能使四边形 $AMDN$ 是平行四边形的是 ______.(填序号)

答案： ①②④

9. 如上右图，在矩形 $ABCD$ 中，$AB = 8$，$BC = 5$，点 $E$ 是边 $AB$ 上的一动点，连接 $EC$，并以 $EC$ 为直角边作等腰直角三角形，其中 $\angle CEF = 90^{\circ}$.
(1) 当点 $F$ 正好在边 $AD$ 上时，$AF =$ ______；
(2) 当点 $E$ 在边 $AB$ 上运动时，$AF$ 的最小值等于 ______.

答案：
3;　$\frac{3\sqrt{2}}{2}$　[提示:　
(1)如图，　当点F在边AD上时，

∵四边形ABCD是矩形，
∴∠A=∠B=90°.
∵∠CEF=90°,
∴∠1+∠2=90°.又
∠2+∠3=90°,
∴∠1=∠3.
∵CE=EF,∠1=∠3,∠A=∠B=90°,
∴△AEF≌△BCE(AAS),
∴AE=BC=
5,
∴AF=BE=AB−AE=8−5=3.　
(2)当点E在边AB上运动时,如图,过点F作FH⊥AB,交AB于
点H,
∵∠CEF=90°,
∴∠1+∠2=90°.又∠2+∠3=90°,
∴∠1=∠3.
∵CE=EF,
∠1=∠3,∠FHE=∠B=90°,
∴△HEF≌△BCE(AAS),
∴FH=BE,EH=CB=5.设FH=BE=x,则
AH=AB−EH−BE=8−5−x=3−x.在Rt△AFH中,AF²=AH²+FH²=(3−x)²+x²=2x²−6x+
9=2(x−$\frac{3}{2}$)²+$\frac{9}{2}$,当x=$\frac{3}{2}$时，AF²最小,最小值为$\frac{9}{2}$,故AF的最小值为$\frac{3\sqrt{2}}{2}$.]

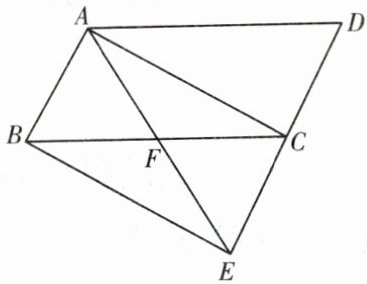
10. 如图，在平行四边形 $ABCD$ 中，$AD = 3$，$CD = 2$.连接 $AC$，过点 $B$ 作 $BE // AC$，交 $DC$ 的延长线于点 $E$，连接 $AE$，交 $BC$ 于点 $F$，若 $\angle AFC = 2\angle D$，求四边形 $ABEC$ 的面积.

答案： 2$\sqrt{5}$ （提示：先证明四边形ABEC是平行四边形，再证明AF = FE = FC = BF，从而得到四边形ABEC是矩形，由勾股定理，得AC = $\sqrt{BC² - AB²}$ = $\sqrt{5}$，
∴ 矩形ABEC的面积为AB × AC = 2$\sqrt{5}$．）

11. 如图，平行四边形 $ABCD$ 的对角线 $AC$，$BD$ 相交于点 $O$，点 $E$，$F$ 在对角线 $BD$ 上，且 $BE = EF = FD$，连接 $AE$，$EC$，$CF$，$FA$.
(1) 求证：四边形 $AECF$ 是平行四边形；
(2) 若 $\triangle ABE$ 的面积等于 $2$，求 $\triangle CFO$ 的面积.

答案： （1）
∵ 四边形ABCD是平行四边形，
∴ OA = OC，OB = OD．
∵ BE = FD，
∴ OB - BE = OD - FD，即 OE = OF，
∴ 四边形AECF是平行四边形．（2）
∵ S△ABE = 2，BE = EF，
∴ S△ABE = S△AEF = 2．
∵ 四边形AECF是平行四边形，
∴ OF = OE，
∴ S△CFO = $\frac{1}{2}$S△CEF = $\frac{1}{2}$S△AEF = $\frac{1}{2}$ × 2 = 1．