第74页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
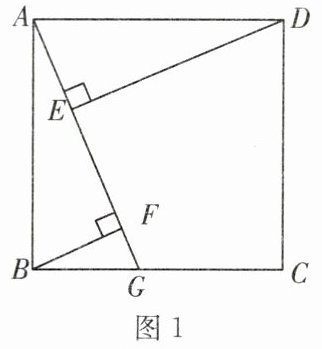
13. 如图1,四边形 $ABCD$ 是正方形,点 $G$ 是 $BC$ 边上任意一点,$DE\perp AG$ 于点 $E$,$BF\perp AG$ 于点 $F$。
(1) 求证:$DE - BF = EF$;
(2) 当点 $G$ 为 $BC$ 边的中点时,试探究线段 $EF$ 与 $GF$ 之间的数量关系,并说明理由;
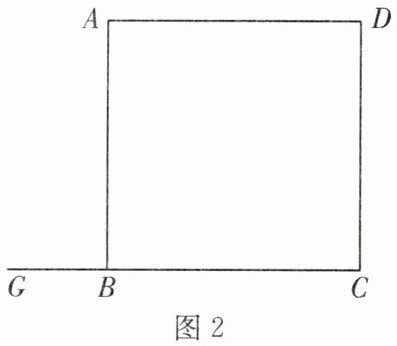
(3) 若点 $G$ 为 $CB$ 延长线上一点,其余条件不变,请你在图2中画出图形,写出此时 $DE$,$BF$,$EF$ 之间的数量关系(不需要证明)。
(1) 求证:$DE - BF = EF$;
(2) 当点 $G$ 为 $BC$ 边的中点时,试探究线段 $EF$ 与 $GF$ 之间的数量关系,并说明理由;
(3) 若点 $G$ 为 $CB$ 延长线上一点,其余条件不变,请你在图2中画出图形,写出此时 $DE$,$BF$,$EF$ 之间的数量关系(不需要证明)。


答案:
(1) 先证 $ \triangle ADE \cong \triangle BAF $,$ \therefore AE = BF $,$ DE = AF $,$ \therefore DE - BF = AF - AE = EF $。
(2) $ EF = 2FG $。理由如下:设 $BG = a$,则 $AB = 2a$,$ \therefore AG = \sqrt{a^{2} + (2a)^{2}} = \sqrt{5}a $,$ \therefore BF = \frac{2a \times a}{\sqrt{5}a} = \frac{2\sqrt{5}}{5}a $,$ GF = \sqrt{a^{2} - \frac{4}{5}a^{2}} = \frac{\sqrt{5}}{5}a $,$ DE = AF = \sqrt{4a^{2} - \frac{4}{5}a^{2}} = \frac{4\sqrt{5}}{5}a $,由
(1) $ EF = DE - BF = \frac{2\sqrt{5}}{5}a $,$ \therefore EF = 2GF $。
(3) 画图略,$ DE + BF = EF $。
(1) 先证 $ \triangle ADE \cong \triangle BAF $,$ \therefore AE = BF $,$ DE = AF $,$ \therefore DE - BF = AF - AE = EF $。
(2) $ EF = 2FG $。理由如下:设 $BG = a$,则 $AB = 2a$,$ \therefore AG = \sqrt{a^{2} + (2a)^{2}} = \sqrt{5}a $,$ \therefore BF = \frac{2a \times a}{\sqrt{5}a} = \frac{2\sqrt{5}}{5}a $,$ GF = \sqrt{a^{2} - \frac{4}{5}a^{2}} = \frac{\sqrt{5}}{5}a $,$ DE = AF = \sqrt{4a^{2} - \frac{4}{5}a^{2}} = \frac{4\sqrt{5}}{5}a $,由
(1) $ EF = DE - BF = \frac{2\sqrt{5}}{5}a $,$ \therefore EF = 2GF $。
(3) 画图略,$ DE + BF = EF $。
查看更多完整答案,请扫码查看


