《2025年暑假作业八年级数学沪科版黄山书社》

12. 如图，老李想用长70m的栅栏，再借助房屋的外墙(外墙足够长)围成一个矩形羊圈ABCD，并在边BC上留一个2m宽的门(建在EF处，另用其他材料).
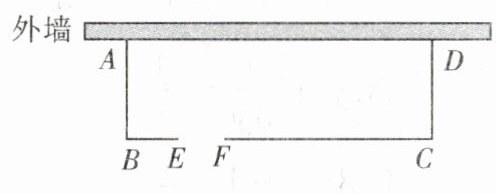
(1) 当羊圈的长和宽分别为多少米时，能围成一个面积为$ 640m^{2} $的羊圈?
(2) 羊圈的面积能达到$ 650m^{2} $吗? 如果能，请给出你的设计方案；如果不能，请说明理由.

答案：
(1) 设矩形 $ ABCD $ 的边 $ AB = x \mathrm{m} $，则边 $ BC = 70 - 2x + 2 = (72 - 2x) \mathrm{m} $。根据题意，得 $ x(72 - 2x) = 640 $，化简得 $ x^2 - 36x + 320 = 0 $，解得 $ x_1 = 16 $，$ x_2 = 20 $。当 $ x = 16 $ 时，$ 72 - 2x = 72 - 32 = 40 $；当 $ x = 20 $ 时，$ 72 - 2x = 72 - 40 = 32 $。答：当羊圈的长为 $ 40 \mathrm{m} $，宽为 $ 16 \mathrm{m} $ 或长为 $ 32 \mathrm{m} $，宽为 $ 20 \mathrm{m} $ 时，能围成一个面积为 $ 640 \mathrm{m}^2 $ 的羊圈。
(2) 不能。理由：由题意，得 $ x(72 - 2x) = 650 $。化简得，$ x^2 - 36x + 325 = 0 $，$ \Delta = (-36)^2 - 4 \times 325 = -4 ＜ 0 $，$ \therefore $ 一元二次方程没有实数根。$ \therefore $ 羊圈的面积不能达到 $ 650 \mathrm{m}^2 $。

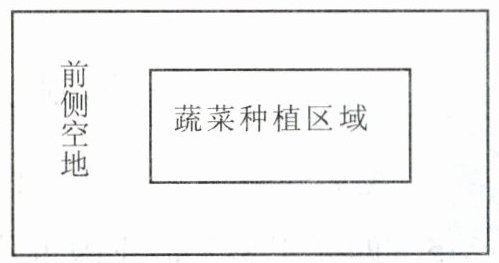
13. 某农场计划建造如图所示的矩形蔬菜温室，要求长与宽的比为$ 2:1 $，在温室内，沿前侧内墙保留3m宽的空地，其他三侧内墙各保留1m宽的通道.当矩形温室的长与宽各为多少时，蔬菜种植区域的面积为$ 288m^{2} $?

答案： 设矩形温室的宽为 $ x \mathrm{m} $，则长为 $ 2x \mathrm{m} $，由题意，得 $ (2x - 4)(x - 2) = 288 $，解得 $ x_1 = -10 $（不合题意，舍去），$ x_2 = 14 $，$ \therefore x = 14 $。故当温室的长为 $ 28 \mathrm{m} $，宽为 $ 14 \mathrm{m} $ 时，蔬菜种植区域的面积为 $ 288 \mathrm{m}^2 $。