《2025年暑假衔接起跑线八升九数学浙教版》

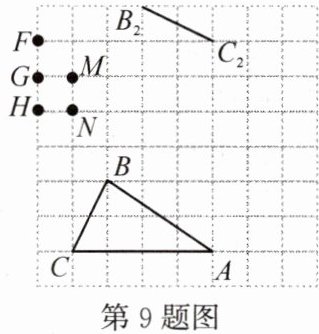
9. 如图所示，△ABC的各顶点都在8×8的网格中的格点(即各个小正方形的顶点)上。
(1)将线段BC绕图中F，G，H，M，N五个格点中的其中一个点可旋转到线段B₂C₂(点B的对应点为B₂)，则旋转中心是点______G；
(2)将△ABC绕点A顺时针旋转90°得到△AB₁C₁，在图中画出△AB₁C₁。

答案： 解:
(1)$G$
(2)图略.

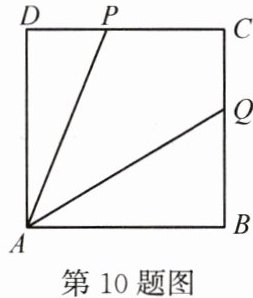
10. 如图所示，点P是正方形ABCD的边CD上一点，连结AP，∠BAP的平分线交BC于点Q，求证：AP=DP+BQ。

答案：
解: 如图所示, 将 $\triangle ABQ$ 绕点 $A$ 逆时针旋转 $90^{\circ}$ 得到 $\triangle ADE$, 则 $\angle EAQ = 90^{\circ}$, $DE = BQ$, $\angle 1 = \angle 2$, $\angle ADE = \angle B = 90^{\circ}$. $\because \angle ADC = 90^{\circ}$, $\therefore \angle ADE + \angle ADC = 180^{\circ}$, $\therefore E$, $D$, $C$ 三点在同一条直线上. $\because AQ$ 平分 $\angle PAB$, $\therefore \angle 3 = \angle 2$. 在 $Rt\triangle ADE$ 中, $\because \angle E + \angle 1 = 90^{\circ}$, $\therefore \angle E = 90^{\circ} - \angle 1 = 90^{\circ} - \angle 2$. 又 $\because \angle PAE + \angle 3 = 90^{\circ}$, $\therefore \angle PAE = 90^{\circ} - \angle 3 = 90^{\circ} - \angle 2$, $\therefore \angle E = \angle PAE$, $\therefore AP = EP$. $\because EP = DP + DE = DP + BQ$, $\therefore AP = DP + BQ$.

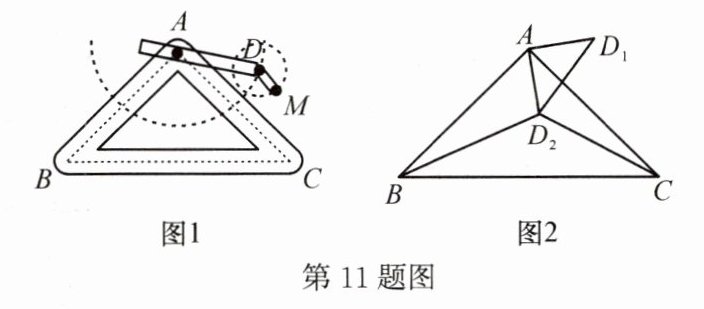
11. 如图1是实验室中的一种摆动装置，BC在地面上，支架ABC是底边为BC的等腰直角三角形，摆动臂AD可绕点A旋转，摆动臂DM可绕点D旋转，AD=30，DM=10。
(1)在旋转过程中，
①当A，D，M三点在同一直线上时，求AM的长；
②当A，D，M三点为同一直角三角形的顶点时，求AM的长；
(2)若摆动臂AD顺时针旋转90°，点D的位置由△ABC外的点D₁转到其内的点D₂处，连结D₁D₂，如图2，此时∠AD₂C=135°，CD₂=60，求BD₂的长。

答案：
解:
(1)①$AM = AD + DM = 40$ 或 $AM = AD - DM = 20$; ②显然 $\angle MAD$ 不能为直角. 当 $\angle AMD$ 为直角时, $AM^{2} = AD^{2} - DM^{2} = 30^{2} - 10^{2} = 800$, $\therefore AM = 20\sqrt{2}$ ($-20\sqrt{2}$ 舍去). 当 $\angle ADM = 90^{\circ}$ 时, $AM^{2} = AD^{2} + DM^{2} = 30^{2} + 10^{2} = 1000$, $\therefore AM = 10\sqrt{10}$ ($-10\sqrt{10}$ 舍去). 综上所述, 满足条件的 $AM$ 长为 $20\sqrt{2}$ 或 $10\sqrt{10}$;
(2)如图, 连结 $CD_{1}$. 由题意, 得 $\angle D_{1}AD_{2} = 90^{\circ}$, $AD_{1} = AD_{2} = 30$, $\therefore \angle AD_{2}D_{1} = 45^{\circ}$, $D_{1}D_{2} = 30\sqrt{2}$. $\because \angle AD_{2}C = 135^{\circ}$, $\therefore \angle CD_{2}D_{1} = 90^{\circ}$, $\therefore CD_{1} = \sqrt{CD_{2}^{2} + D_{1}D_{2}^{2}} = 30\sqrt{6}$. $\because \angle BAC = \angle D_{1}AD_{2} = 90^{\circ}$, $\therefore \angle BAC - \angle CAD_{2} = \angle D_{2}AD_{1} - \angle CAD_{2}$, 即 $\angle BAD_{2} = \angle CAD_{1}$. 又 $\because AB = AC$, $AD_{2} = AD_{1}$, $\therefore \triangle BAD_{2} \cong \triangle CAD_{1}(SAS)$, $\therefore BD_{2} = CD_{1} = 30\sqrt{6}$.