《2025年暑假衔接起跑线八升九数学浙教版》

1. 销售中的数量关系:销售利润=销售收入-成本;总利润=销售量×每个的利润.

答案： 销售收入 成本 销售量 利润

2. 求二次函数的最大(小)值时,应根据实际情况调整自变量的取值,使得在自变量允许的取值范围内,函数取得最大或最小值.

答案： 实际情况 取值范围

例1 某商场要经营一种新上市的文具,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润$w$(元)与销售单价$x$(元)之间的函数表达式;
(2)求销售单价为多少元时,该文具每天的销售利润最大?
(3)商场的营销部结合上述情况,提出了A,B两种营销方案:
方案A:该文具的销售单价高于进价且不超过30元;
方案B:每天销售量不少于10件,且每件文具的利润至少为25元.
请比较哪种方案的最大利润更高,并说明理由.

答案： 【解析】：
1. 对于（1），根据利润 =（单价 - 进价）× 销售量来求函数表达式。已知进价为$20$元/件，销售单价为$x$元，当销售单价是$25$元时，每天的销售量为$250$件，销售单价每上涨$1$元，每天的销售量就减少$10$件，那么销售量为$250 - 10\times(x - 25)$件，所以$w=(x - 20)[250 - 10\times(x - 25)]$，展开式子$(x - 20)(250 - 10x + 250)=(x - 20)(500 - 10x)=-10x^{2}+700x - 10000$，即$w$与$x$之间的函数表达式是$w=-10x^{2}+700x - 10000$。
2. 对于（2），将函数$w=-10x^{2}+700x - 10000$进行配方，$w=-10(x^{2}-70x + 1000)=-10(x^{2}-70x+35^{2}-1225 + 1000)=-10[(x - 35)^{2}-225]=-10(x - 35)^{2}+2250$。因为二次项系数$a=-10\lt0$，所以抛物线开口向下，函数有最大值，当$x = 35$时，$w_{最大值}=2250$，即当销售单价为$35$元时，该文具每天的销售利润最大。
3. 对于（3）：
方案A：由条件$20\lt x\leqslant30$，因为$a=-10\lt0$，对称轴是$x = 35$，抛物线开口向下，在对称轴左侧$w$随$x$的增大而增大，所以当$x = 30$时，$w$取最大值，把$x = 30$代入$w=-10(x - 35)^{2}+2250$，可得$w_{A最大值}=-10\times(30 - 35)^{2}+2250=-10\times25 + 2250 = 2000$元。
方案B：根据条件列不等式组$\begin{cases}x\geqslant45\\250 - 10\times(x - 25)\geqslant10\end{cases}$，解第一个不等式得$x\geqslant45$，解第二个不等式$250-10x + 250\geqslant10$，即$500-10x\geqslant10$，$10x\leqslant490$，解得$x\leqslant49$，所以不等式组的解集为$45\leqslant x\leqslant49$。因为在对称轴$x = 35$右侧$w$随$x$的增大而减小，所以当$x = 45$时，$w$取最大值，把$x = 45$代入$w=-10(x - 35)^{2}+2250$，可得$w_{B最大值}=-10\times(45 - 35)^{2}+2250=-10\times100 + 2250 = 1250$元。比较$2000$与$1250$大小，$2000\gt1250$，所以方案A的最大利润更高。
【答案】：（1）$w=-10x^{2}+700x - 10000$；（2）$35$元；（3）方案A的最大利润更高，理由：方案A最大利润为$2000$元，方案B最大利润为$1250$元，$2000\gt1250$。

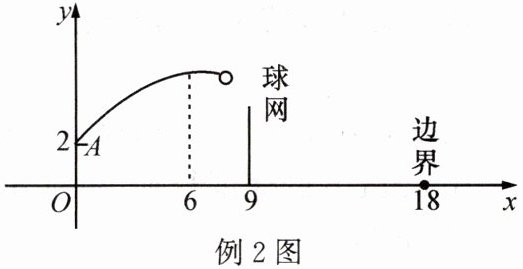
例2 如图,排球运动员站在$O$处练习发球,将球从点$O$正上方2m的$A$处发出,把球看成点,其运行的高度$y$(m)与运行的水平距离$x$(m)满足表达式$y=a(x-6)^{2}+h$.已知球网与点$O$的水平距离为9m,高度为2.43m,球场的边界距点$O$的水平距离为18m.
(1)当$h=2.6$时,求$y$与$x$的函数表达式(不要求写出自变量$x$的取值范围);
$y=-\frac{1}{60}(x-6)^{2}+2.6$
(2)当$h=2.6$时,球能否越过球网? 球会不会出界? 请说明理由;
球能越过球网；球会出界
(3)若球一定能越过球网,又不出边界,求$h$的取值范围.
$h\geqslant\frac{8}{3}$

答案： 解:
(1)当$h=2.6$时,设$y=a(x-6)^{2}+2.6$.$\because$过点$(0,2)$,
$\therefore36a+2.6=2$,解得$a=-\frac{1}{60}$,$\therefore y=-\frac{1}{60}(x-6)^{2}+2.6$;

(2)当$x=9$时,$y=-\frac{1}{60}\times9+2.6=2.45＞2.43$,$\therefore$球能越
过球网;当$x=18$时,$y=-\frac{1}{60}\times(18-6)^{2}+2.6=0.2＞0$,$\therefore$球会出界;

(3)设$y=a(x-6)^{2}+h$.当过点$(0,2)$,$(9,2.43)$时,得$\begin{cases}36a+h=2,\\9a+h=2.43,\end{cases}$解得$h=\frac{193}{75}$.$\because$要越过球网,$\therefore h\geqslant\frac{193}{75}$.当过点$(0,2)$,$(18,0)$时,得$\begin{cases}36a+h=2,\\144a+h=0,\end{cases}$解得$h=\frac{8}{3}$.$\because$球不出边界,$\therefore h\geqslant\frac{8}{3}$.
$\because\begin{cases}h\geqslant\frac{193}{75},\\h\geqslant\frac{8}{3},\end{cases}$$\therefore h\geqslant\frac{8}{3}$.