第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 下列各组式子中,为同类项的是(
A.$ x 与 y $
B.$ 2a^{2}b 与 ab^{2} $
C.$ x^{2}y^{3} 与 5x^{2}z^{3} $
D.$ 2xy^{2} 与 -3xy^{2} $
D
)A.$ x 与 y $
B.$ 2a^{2}b 与 ab^{2} $
C.$ x^{2}y^{3} 与 5x^{2}z^{3} $
D.$ 2xy^{2} 与 -3xy^{2} $
答案:
解:同类项是指所含字母相同,并且相同字母的指数也相同的项。
A. $x$ 与 $y$ 所含字母不同,不是同类项;
B. $2a^{2}b$ 与 $ab^{2}$ 相同字母的指数不同,不是同类项;
C. $x^{2}y^{3}$ 与 $5x^{2}z^{3}$ 所含字母不同,不是同类项;
D. $2xy^{2}$ 与 $-3xy^{2}$ 所含字母相同,相同字母的指数也相同,是同类项。
答案:D
A. $x$ 与 $y$ 所含字母不同,不是同类项;
B. $2a^{2}b$ 与 $ab^{2}$ 相同字母的指数不同,不是同类项;
C. $x^{2}y^{3}$ 与 $5x^{2}z^{3}$ 所含字母不同,不是同类项;
D. $2xy^{2}$ 与 $-3xy^{2}$ 所含字母相同,相同字母的指数也相同,是同类项。
答案:D
2. 下列说法中,正确的是(
A.$ \frac{m^{2}n}{2} $不是整式
B.$ -\frac{3abc}{2} 的系数是 -\frac{3}{2} $,次数是3
C.$ 3a^{2}bc 与 bca^{2} $不是同类项
D.$ \frac{1}{x}+\frac{1}{y} $是多项式
B
)A.$ \frac{m^{2}n}{2} $不是整式
B.$ -\frac{3abc}{2} 的系数是 -\frac{3}{2} $,次数是3
C.$ 3a^{2}bc 与 bca^{2} $不是同类项
D.$ \frac{1}{x}+\frac{1}{y} $是多项式
答案:
解:A. $\frac{m^{2}n}{2}$是整式,A错误;
B. $-\frac{3abc}{2}$的系数是$-\frac{3}{2}$,次数是3,B正确;
C. $3a^{2}bc$与$bca^{2}$是同类项,C错误;
D. $\frac{1}{x}+\frac{1}{y}$不是多项式,D错误。
故选B。
B. $-\frac{3abc}{2}$的系数是$-\frac{3}{2}$,次数是3,B正确;
C. $3a^{2}bc$与$bca^{2}$是同类项,C错误;
D. $\frac{1}{x}+\frac{1}{y}$不是多项式,D错误。
故选B。
3. $ -3x^{2}y+\frac{1}{2}x^{2}y $的结果为(
A.$ -\frac{5}{2}x^{4}y^{2} $
B.$ \frac{5}{2}x^{4}y^{2} $
C.$ -\frac{5}{2}x^{2}y $
D.$ \frac{5}{2}x^{2}y $
C
)A.$ -\frac{5}{2}x^{4}y^{2} $
B.$ \frac{5}{2}x^{4}y^{2} $
C.$ -\frac{5}{2}x^{2}y $
D.$ \frac{5}{2}x^{2}y $
答案:
解:$-3x^{2}y+\frac{1}{2}x^{2}y$
$=(-3+\frac{1}{2})x^{2}y$
$=-\frac{5}{2}x^{2}y$
答案:C
$=(-3+\frac{1}{2})x^{2}y$
$=-\frac{5}{2}x^{2}y$
答案:C
4. 今年苹果的价格比去年便宜了20%,已知去年苹果的价格是每千克$ a $元,则今年每千克苹果的价格是(
A.$ \frac{a}{20\%} $元
B.$ (1 - 20\%)a $元
C.$ 20\%a $元
D.$ \frac{a}{1 - 20\%} $元
B
)A.$ \frac{a}{20\%} $元
B.$ (1 - 20\%)a $元
C.$ 20\%a $元
D.$ \frac{a}{1 - 20\%} $元
答案:
解:去年苹果价格为每千克$a$元,今年比去年便宜$20\%$,则今年价格是去年的$(1 - 20\%)$,所以今年每千克苹果价格为$(1 - 20\%)a$元。
答案:B
答案:B
5. 一个多项式加上$ -2a + 7 等于 3a^{2} + a + 1 $,则这个多项式是(
A.$ 3a^{2} - a - 6 $
B.$ 3a^{2} + 3a + 8 $
C.$ 3a^{2} + 3a - 6 $
D.$ -3a^{2} - 3a + 6 $
C
)A.$ 3a^{2} - a - 6 $
B.$ 3a^{2} + 3a + 8 $
C.$ 3a^{2} + 3a - 6 $
D.$ -3a^{2} - 3a + 6 $
答案:
解:设这个多项式为$M$,由题意得:
$M + (-2a + 7) = 3a^{2} + a + 1$
$M = 3a^{2} + a + 1 - (-2a + 7)$
$M = 3a^{2} + a + 1 + 2a - 7$
$M = 3a^{2} + 3a - 6$
答案:C
$M + (-2a + 7) = 3a^{2} + a + 1$
$M = 3a^{2} + a + 1 - (-2a + 7)$
$M = 3a^{2} + a + 1 + 2a - 7$
$M = 3a^{2} + 3a - 6$
答案:C
6. 已知$ a - 2b = 3 $,则$ 3(a - b) - (a + b) $的值为(
A.3
B.6
C.-3
D.-6
B
)A.3
B.6
C.-3
D.-6
答案:
解:$3(a - b) - (a + b)$
$=3a - 3b - a - b$
$=2a - 4b$
$=2(a - 2b)$
因为$a - 2b = 3$,所以原式$=2×3 = 6$
答案:B
$=3a - 3b - a - b$
$=2a - 4b$
$=2(a - 2b)$
因为$a - 2b = 3$,所以原式$=2×3 = 6$
答案:B
7. 一家三口准备参加旅行团外出旅游,甲旅行社告知:“父母买全票,女儿按半价优惠。”乙旅行社告知:“家庭旅游可按团体票价收费,即每人均按全价的$ \frac{5}{6} $收费。”若两家旅行社的票价相同,那么(
A.甲比乙优惠
B.乙比甲优惠
C.甲与乙相同
D.不确定
C
)A.甲比乙优惠
B.乙比甲优惠
C.甲与乙相同
D.不确定
答案:
设两家旅行社的全票价均为$x$。
甲旅行社费用:$2x + \frac{1}{2}x = 2.5x$
乙旅行社费用:$3×\frac{5}{6}x = 2.5x$
因为$2.5x = 2.5x$,所以甲与乙相同。
C
甲旅行社费用:$2x + \frac{1}{2}x = 2.5x$
乙旅行社费用:$3×\frac{5}{6}x = 2.5x$
因为$2.5x = 2.5x$,所以甲与乙相同。
C
8. 如图,边长为$ (m + 3) 的正方形纸片剪出一个边长为 m $的正方形之后,剩余部分又剪拼成一个矩形(不重叠无缝隙),若拼成的矩形一边长为3,则另一边长是(
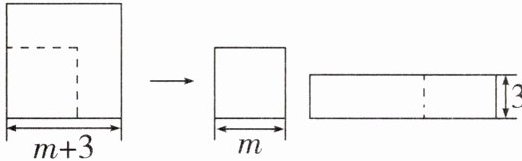
A.$ 2m + 3 $
B.$ 2m + 6 $
C.$ m + 3 $
D.$ m + 6 $
A
) 
A.$ 2m + 3 $
B.$ 2m + 6 $
C.$ m + 3 $
D.$ m + 6 $
答案:
解:大正方形面积为$(m + 3)^2 = m^2 + 6m + 9$,小正方形面积为$m^2$,剩余部分面积为$m^2 + 6m + 9 - m^2 = 6m + 9$。
矩形一边长为3,设另一边长为$x$,则$3x = 6m + 9$,解得$x = 2m + 3$。
A
矩形一边长为3,设另一边长为$x$,则$3x = 6m + 9$,解得$x = 2m + 3$。
A
9. 已知两个单项式$ -2a^{2}b^{m + 1} 与 na^{2}b^{4} $的和为0,则$ m + n $的值是______。
5
答案:
解:因为两个单项式的和为0,所以它们是同类项且系数互为相反数。
对于同类项,相同字母的指数相同,所以$m + 1 = 4$,解得$m = 3$。
系数互为相反数,所以$-2 + n = 0$,解得$n = 2$。
则$m + n = 3 + 2 = 5$。
5
对于同类项,相同字母的指数相同,所以$m + 1 = 4$,解得$m = 3$。
系数互为相反数,所以$-2 + n = 0$,解得$n = 2$。
则$m + n = 3 + 2 = 5$。
5
10. 计算:(1)$ 3a^{2}b - a^{2}b = $
(2)$ 3x - [5x - 4(2x - 1)] = $
$2a^{2}b$
;(2)$ 3x - [5x - 4(2x - 1)] = $
$6x - 4$
。
答案:
(1) $3a^{2}b - a^{2}b = (3 - 1)a^{2}b = 2a^{2}b$
(2) $3x - [5x - 4(2x - 1)]$
$= 3x - [5x - 8x + 4]$
$= 3x - (-3x + 4)$
$= 3x + 3x - 4$
$= 6x - 4$
(1) $3a^{2}b - a^{2}b = (3 - 1)a^{2}b = 2a^{2}b$
(2) $3x - [5x - 4(2x - 1)]$
$= 3x - [5x - 8x + 4]$
$= 3x - (-3x + 4)$
$= 3x + 3x - 4$
$= 6x - 4$
11. 按照如图操作,若输入$ x $的值是9,则输出的值是______。


193
答案:
解:输入x=9,
第一步:9+5=14,
第二步:14²=196,
第三步:196-3=193,
输出的值是193。
193
第一步:9+5=14,
第二步:14²=196,
第三步:196-3=193,
输出的值是193。
193
12. 若多项式$ 2(x^{2} - xy + y^{2}) - (3x^{2} - axy + y^{2}) $中不含 $xy $项,则$ a = $______。
2
答案:
解:$2(x^{2} - xy + y^{2}) - (3x^{2} - axy + y^{2})$
$=2x^{2}-2xy+2y^{2}-3x^{2}+axy-y^{2}$
$=-x^{2}+(a-2)xy+y^{2}$
因为多项式中不含$xy$项,所以$a-2=0$,解得$a=2$。
2
$=2x^{2}-2xy+2y^{2}-3x^{2}+axy-y^{2}$
$=-x^{2}+(a-2)xy+y^{2}$
因为多项式中不含$xy$项,所以$a-2=0$,解得$a=2$。
2
查看更多完整答案,请扫码查看


