《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

16. 如图,从边长为$(a+1)cm的正方形纸片中剪去一个边长为(a-1)cm的正方形(a＞1)$,剩余部分沿虚线剪开并拼成一个长方形(不重叠无缝隙),则该长方形的面积是______$cm^{2}$.

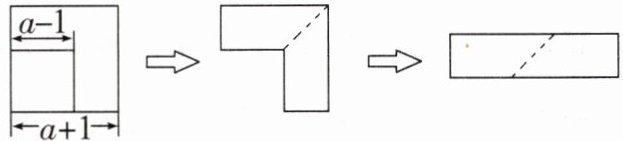
4a

答案： 解：剩余部分的面积为大正方形面积减去小正方形面积，即
$(a+1)^2 - (a-1)^2$
展开计算：
$\begin{aligned}&(a^2 + 2a + 1) - (a^2 - 2a + 1)\\=&a^2 + 2a + 1 - a^2 + 2a - 1\\=&4a\end{aligned}$
因为拼成的长方形面积等于剩余部分面积，所以长方形的面积是$4a$ $cm^2$。
$4a$

17. (8分)计算下列各式：
(1)$(-5ab^{2}x)\cdot(-\frac{3}{10}a^{2}bx^{3}y)$；
(2)$(a+3)^{2}+a(4-a)$；
(3)$(a-2b+3)(a+2b-3)$；
(4)$15\frac{2}{3}×14\frac{1}{3}$.

答案：
(1) 原式$=(-5)×(-\frac{3}{10})(a\cdot a^{2})(b^{2}\cdot b)(x\cdot x^{3})\cdot y=\frac{3}{2}a^{3}b^{3}x^{4}y$；
(2) 原式$=a^{2}+6a + 9+4a - a^{2}=10a + 9$；
(3) 原式$=[a-(2b - 3)][a+(2b - 3)]=a^{2}-(2b - 3)^{2}=a^{2}-4b^{2}+12b - 9$；
(4) 原式$=(15+\frac{2}{3})×(15-\frac{2}{3})=15^{2}-(\frac{2}{3})^{2}=225-\frac{4}{9}=224\frac{5}{9}$。

18. (12分)(1)先化简,再求值：$(1+a)(1-a)+(a-2)^{2}$,其中$a= -3$；
(2)已知$A= 2x+y$,$B= 2x-y$,计算$A^{2}-B^{2}$；
(3)已知$a≠b$,且$a(a+2)= b(b+2)$,求$a+b$的值.

答案：
(1) 原式$=1 - a^{2} + a^{2} - 4a + 4 = -4a + 5$，当$a = -3$时，原式$=-4×(-3) + 5 = 12 + 5 = 17$；
(2) $A^{2}-B^{2}=(2x + y)^{2}-(2x - y)^{2}=[(2x + y)+(2x - y)][(2x + y)-(2x - y)]=(4x)(2y)=8xy$；
(3) 由$a(a + 2)=b(b + 2)$得$a^{2}+2a = b^{2}+2b$，$a^{2}-b^{2}+2a - 2b = 0$，$(a - b)(a + b)+2(a - b)=0$，$(a - b)(a + b + 2)=0$，因为$a≠b$，所以$a + b + 2 = 0$，即$a + b=-2$。