《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

12. “同位角相等”的逆命题是相等的角是同位角.

答案： 相等的角是同位角

13. 若$ 2 ^ { x } = 3 $,$ 4 ^ { y } = 5 $,则$ 2 ^ { x - 2 y } $的值为$\frac{3}{5}$.

答案： 解：因为$4^y = (2^2)^y = 2^{2y} = 5$，且$2^x = 3$，所以$2^{x - 2y} = 2^x ÷ 2^{2y} = 3 ÷ 5 = \frac{3}{5}$。
$\frac{3}{5}$

14. 已知关于$ x $的不等式组 $\left\{ \begin{array} { l } { a - x ＞ 0 }, \\ { 3 x + 5 ＞ 0 } \end{array} \right.$ 的整数解共有4个,则$ a $的取值范围是$2 ＜ a \leq 3$.

答案： 解：解不等式组$\left\{ \begin{array}{l} a - x ＞ 0 \\ 3x + 5 ＞ 0 \end{array} \right.$
解第一个不等式：$a - x ＞ 0$，得$x ＜ a$
解第二个不等式：$3x + 5 ＞ 0$，得$x ＞ -\frac{5}{3}$
所以不等式组的解集为$-\frac{5}{3} ＜ x ＜ a$
因为不等式组的整数解共有4个，且大于$-\frac{5}{3}$的连续整数为$-1, 0, 1, 2$
所以这4个整数解为$-1, 0, 1, 2$
则$a$的取值范围是$2 ＜ a \leq 3$
$2 ＜ a \leq 3$

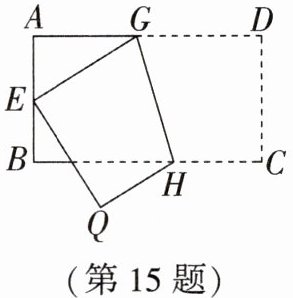
15. 如图,将长方形$ ABCD 沿 GH $折叠,点$ C 落在点 Q $处,点$ D 落在 AB 边上的点 E $处,若$ \angle AGE = 32 ^ { \circ } $,则$ \angle GHC = $106$ ^ { \circ } $.

答案： 解：
∵∠AGE=32°，
∴∠DGE=180°-∠AGE=148°。
由折叠性质得∠DGH=∠EGH=∠DGE/2=74°。
∵四边形ABCD是长方形，
∴AD//BC，
∴∠GHC+∠DGH=180°，
∴∠GHC=180°-∠DGH=106°。
106

16. 如图,在$ \triangle ABC $中,点$ D 在边 BC $上,$ AD \perp BC $,$ AD = 2 $,$ BD = 3 $,$ CD = 4 $,将$ \triangle ABC 绕着点 D $旋转,使得点$ A 的对应点 A ^ { \prime } 落在边 BC $上,点$ B $,$ C 的对应点分别是点 B ^ { \prime } $,$ C ^ { \prime } $,则$ \triangle A ^ { \prime } B ^ { \prime } C $的面积等于____.

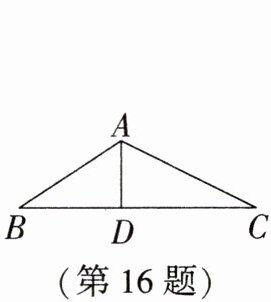
3或9

答案： 解：
情况1：点$A'$在$D$左侧
$\because AD=2$，旋转后$A'D=AD=2$，$BD=3$，
$\therefore BA'=BD - A'D=3 - 2=1$，$A'C=A'D + DC=2 + 4=6$，
$\because$旋转后$B'D=BD=3$，$\angle B'DA'=\angle BDA=90^\circ$，
$\therefore S_{\triangle A'B'C}=\frac{1}{2} × A'C × B'D=\frac{1}{2} × 6 × 3=9$。
情况2：点$A'$在$D$右侧
$\because A'D=AD=2$，$CD=4$，
$\therefore A'C=CD - A'D=4 - 2=2$，$BA'=BD + A'D=3 + 2=5$，
$\because$旋转后$B'D=BD=3$，$\angle B'DA'=\angle BDA=90^\circ$，
$\therefore S_{\triangle A'B'C}=\frac{1}{2} × A'C × B'D=\frac{1}{2} × 2 × 3=3$。
综上，$\triangle A'B'C$的面积等于$3$或$9$。
答案：$3$或$9$

17. (4分)解方程组或不等式组:
(1)$ \left\{ \begin{array} { l } { 2 x - y = 3 }, \\ { 3 x + 4 y = 10 } \end{array} \right. $
(2)解不等式组$ \left\{ \begin{array} { l } { 3 x + 1 ＜ 2 ( x + 2 ) }, \\ { - \frac { 1 } { 3 } x \leq \frac { 5 } { 3 } x + 2 }, \end{array} \right. $并求出其整数解.

答案：
(1)解：$\left\{\begin{array}{l}2x - y = 3①\\3x + 4y = 10②\end{array}\right.$
由①得$y = 2x - 3$③
把③代入②得$3x + 4(2x - 3)=10$
$3x + 8x - 12 = 10$
$11x = 22$
$x = 2$
把$x = 2$代入③得$y = 2×2 - 3 = 1$
所以方程组的解为$\left\{\begin{array}{l}x = 2\\y = 1\end{array}\right.$
(2)解：$\left\{\begin{array}{l}3x + 1 ＜ 2(x + 2)①\\-\frac{1}{3}x\leq\frac{5}{3}x + 2②\end{array}\right.$
解不等式①：$3x + 1 ＜ 2x + 4$
$3x - 2x ＜ 4 - 1$
$x ＜ 3$
解不等式②：$-\frac{1}{3}x - \frac{5}{3}x\leq2$
$-2x\leq2$
$x\geq - 1$
所以不等式组的解集为$-1\leq x ＜ 3$
整数解为$x = -1,0,1,2$

18. (6分)先化简,再求值:
(1)$ ( a + 2 ) ^ { 2 } + ( 1 - a ) ( 1 + a ) $,其中$ a = - \frac { 3 } { 4 } $;
(2)$ [ ( x - 2 y ) ^ { 2 } - ( x + y ) ( 3 x - y ) - 5 y ^ { 2 } ] ÷ 2 x $,其中$ x = - 2 $,$ y = 1 $.

答案：
(1) 原式$=a^2 + 4a + 4 + 1 - a^2 = 4a + 5$，当$a=-\frac{3}{4}$时，原式$=4×(-\frac{3}{4}) + 5 = -3 + 5 = 2$；
(2) 原式$=(x^2 - 4xy + 4y^2 - 3x^2 + xy - 3xy + y^2 - 5y^2)÷2x = (-2x^2 - 6xy)÷2x = -x - 3y$，当$x=-2$，$y=1$时，原式$=-(-2) - 3×1 = 2 - 3 = -1$。

19. (8分)对于一个任意的四位数$ M $,若$ M $的千位上的数与个位上的数之和等于百位上的数与十位上的数之和,我们称这样的四位数为“稳定数”.例如:四位数3197,因为$ 3 + 7 = 1 + 9 $,所以四位数3197是稳定数.
(1)填空:2025____不是稳定数(填“是”或“不是”).
(2)已知一个稳定数的千位上的数为1,百位上的数为9,求这个稳定数.设十位上的数为 $a$，个位上的数为 $b$，根据题意，得 $1 + b = 9 + a$，即 $b - a = 8$。
因为 $a$、$b$ 为一位数（$0 \leq a \leq 9$，$0 \leq b \leq 9$），所以
$\begin{cases} a = 0, \\ b = 8 \end{cases}$ 或 $\begin{cases} a = 1, \\ b = 9. \end{cases}$
故这个稳定数为 1908 或 1919。
(3)命题“两个稳定数的和仍是稳定数”是真命题还是假命题?请说明理由.假命题。
理由：例如，2817（$2+7=8+1$）和 2222（$2+2=2+2$）都是稳定数，它们的和为 $2817 + 2222 = 5039$。
因为 $5 + 9 = 14$，$0 + 3 = 3$，且 $14 \neq 3$，所以 5039 不是稳定数。
因此，两个稳定数的和不一定是稳定数。

答案：
(1) 不是
(2) 设十位上的数为 $a$，个位上的数为 $b$，根据题意，得 $1 + b = 9 + a$，即 $b - a = 8$。
因为 $a$、$b$ 为一位数（$0 \leq a \leq 9$，$0 \leq b \leq 9$），所以
$\begin{cases} a = 0, \\ b = 8 \end{cases}$ 或 $\begin{cases} a = 1, \\ b = 9. \end{cases}$
故这个稳定数为 1908 或 1919。
(3) 假命题。
理由：例如，2817（$2+7=8+1$）和 2222（$2+2=2+2$）都是稳定数，它们的和为 $2817 + 2222 = 5039$。
因为 $5 + 9 = 14$，$0 + 3 = 3$，且 $14 \neq 3$，所以 5039 不是稳定数。
因此，两个稳定数的和不一定是稳定数。