《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

21. (8分)如图①,直线AB与CD交于点O,且$ ∠EOA= 90^{\circ} $.

(1)若点B在点O的正东方向上,点D在点O的北偏东$ 20^{\circ} $方向上,则点C在点O的____方向上;
(2)判断$ ∠AOC 与 ∠EOD $的数量关系并说明理由;
(3)如图②,OM是$ ∠BOC $的平分线,设$ ∠EOD= α(α＜90^{\circ}) $.
①求$ ∠BOM $的度数(用含α的代数式表示);
②直线CD由图②位置开始,绕点O以每秒$ \frac{1}{10}α $的速度顺时针旋转t秒(旋转角度始终小于$ 180^{\circ} $),请你直接写出$ ∠BOM $的度数(用含α,t的代数式表示).

答案：

(1)南偏西20°
(2)∠AOC + ∠EOD = 90°。理由如下：
∵直线AB与CD交于点O，且∠EOA = 90°，∠AOC + ∠AOE + ∠EOD = 180°，
∴∠AOC + ∠EOD = 180° - ∠AOE = 180° - 90° = 90°
(3)①由
(2)可知，∠AOC + ∠EOD = 90°，
∵∠EOD = α，
∴∠AOC = 90° - ∠EOD = 90° - α。
∵∠AOC + ∠BOC = 180°，
∴∠BOC = 180° - ∠AOC = 180° - (90° - α) = 90° + α
∵OM是∠BOC的平分线，
∴∠BOM = $\frac{1}{2}$∠BOC = $\frac{1}{2}$(90° + α) = 45° + $\frac{1}{2}$α
②当点C在直线AB下方时，∠BOM = 45° + $\frac{1}{2}$α + $\frac{1}{20}$α·t；当点C在直线AB上时，∠BOM = 90°；当点C在直线AB上方时，∠BOM = 135° - $\frac{1}{2}$α - $\frac{1}{20}$α·t
提示：
∵∠EOD = α，
∴∠BOD = 90° - α，
∴∠BOC = 180° - ∠BOD = 180° - (90° - α) = 90° + α。设CD旋转后得到C'D'，则OM是∠BOC'的平分线，∠COC' = $\frac{1}{10}$α·t
Ⅰ. 如图①，当点C'在直线AB下方时，
　
则∠BOC' = ∠BOC + ∠COC' = 90° + α + $\frac{1}{10}$α·t。
∵OM是∠BOC'的平分线，
∴∠BOM = $\frac{1}{2}$∠BOC' = $\frac{1}{2}$(90° + α + $\frac{1}{10}$α·t) = 45° + $\frac{1}{2}$α + $\frac{1}{20}$α·t
Ⅱ. 当点C'在直线AB上时，∠BOC = ∠BOC' = 180°。
∵OM是∠BOC'的平分线，
∴∠BOM = 90°
Ⅲ. 当点C'在直线AB上方时，则∠BOC' = 360° - (∠BOC + ∠COC') = 360° - (90° + α + $\frac{1}{10}$α·t) = 270° - α - $\frac{1}{10}$α·t。
∵OM是∠BOC'的平分线，
∴∠BOM = $\frac{1}{2}$∠BOC' = $\frac{1}{2}$(270° - α - $\frac{1}{10}$α·t) = 135° - $\frac{1}{2}$α - $\frac{1}{20}$α·t。综上所述，∠BOM = 45° + $\frac{1}{2}$α + $\frac{1}{20}$α·t或135° - $\frac{1}{2}$α - $\frac{1}{20}$α·t或90°

22. (8分)已知:在$ △ABC $中,$ ∠C＞∠B $,AE平分$ ∠BAC $.
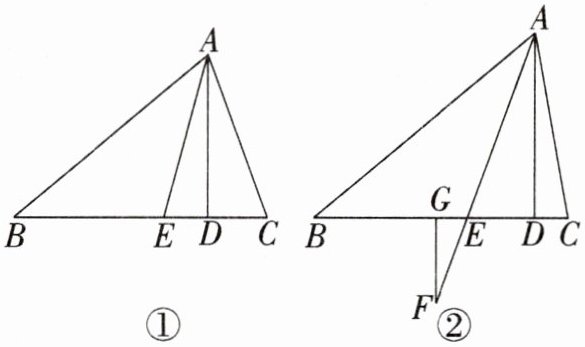
(1)如图①,$ AD⊥BC $于D,若$ ∠C= 70^{\circ} $,$ ∠B= 40^{\circ} $,求$ ∠DAE $的度数;
(2)若$ △ABC $中,$ ∠B= α $,$ ∠C= β(α＜β) $.请根据第(1)问的结果,大胆猜想$ ∠DAE $与α,β的等量关系,并说明理由;
(3)如图②所示,在$ △ABC $中,$ AD⊥BC $,AE平分$ ∠BAC $,F为AE延长线上任一点,过F点作$ FG⊥BC $于G,$ ∠B= 40^{\circ} $,$ ∠C= 80^{\circ} $.请你运用(2)中的结论,求$ ∠EFG $的度数.

答案：
(1)
∵∠C = 70°，∠B = 40°，
∴∠BAC = 180° - (∠B + ∠C) = 180° - (40° + 70°) = 70°。
∵AE平分∠BAC，
∴∠CAE = $\frac{1}{2}$∠BAC = $\frac{1}{2}$×70° = 35°。
∵AD⊥BC，
∴∠ADC = 90°。
∵∠C = 70°，
∴∠DAC = 180° - 90° - 70° = 20°，
∴∠DAE = ∠CAE - ∠CAD = 35° - 20° = 15°
(2)∠DAE = $\frac{1}{2}$β - $\frac{1}{2}$α
理由如下：
∵∠C = β，∠B = α，
∴∠BAC = 180° - (∠B + ∠C) = 180° - α - β
∵AE平分∠BAC，
∴∠CAE = $\frac{1}{2}$∠BAC = $\frac{1}{2}$×(180° - α - β) = 90° - $\frac{1}{2}$α - $\frac{1}{2}$β
∵AD⊥BC，
∴∠ADC = 90°。
∵∠C = β，
∴∠CAD = 180° - 90° - β = 90° - β，
∴∠DAE = ∠CAE - ∠CAD = 90° - $\frac{1}{2}$α - $\frac{1}{2}$β - (90° - β) = $\frac{1}{2}$β - $\frac{1}{2}$α
(3)
∵∠B = 40°，∠C = 80°，
∴∠DAE = $\frac{1}{2}$×80° - $\frac{1}{2}$×40° = 20°。
∵AD⊥BC，FG⊥BC，
∴∠ADE = ∠FGE = 90°，
∴AD//FG，
∴∠EFG = ∠DAE = 20°