《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

9. 已知线段 AB = 10 cm,BC = 5 cm,A,B,C 三点在同一条直线上,则 AC = 5cm或15cm。

答案： 解：当点C在线段AB上时，AC=AB-BC=10-5=5cm；
当点C在线段AB的延长线上时，AC=AB+BC=10+5=15cm。
故AC=5cm或15cm。

10. 如图是一个几何体的三视图,由图中数据计算此几何体的表面积为 28π。

答案： 解：由三视图可知该几何体为圆柱，底面直径为4，高为5。
底面半径 $ r = \frac{4}{2} = 2 $
底面积 $ S_{底} = \pi r^2 = \pi × 2^2 = 4\pi $，两个底面积为 $ 2 × 4\pi = 8\pi $
侧面积 $ S_{侧} = 2\pi r h = 2\pi × 2 × 5 = 20\pi $
表面积 $ S = 8\pi + 20\pi = 28\pi $
28π

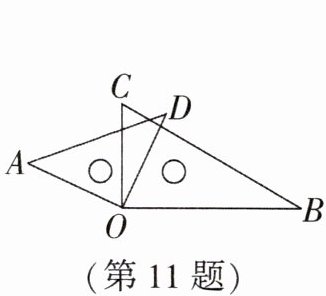
11. 如图,将一副三角板叠在一起,使它们的直角顶点重合于 O 点,且∠AOB = 155°,则∠COD = 25°。

答案： 解：由题意知，∠AOC=∠BOD=90°。
因为∠AOB=∠AOC+∠BOD-∠COD，
所以∠COD=∠AOC+∠BOD-∠AOB=90°+90°-155°=25°。
25°

12. 如图,线段 AB 上有两点 M,N,点 M 分 AB 为 1 : 2 两部分,点 N 分 AB 为 1 : 3 两部分,若 MN = 2,则 AB 的长为 24。

答案： 解：设AB的长为x。
因为点M分AB为1:2两部分，所以AM = $\frac{1}{3}x$，MB = $\frac{2}{3}x$。
因为点N分AB为1:3两部分，所以AN = $\frac{1}{4}x$，NB = $\frac{3}{4}x$。
由图可知，MN = AM - AN，即$\frac{1}{3}x - \frac{1}{4}x = 2$。
$\frac{4}{12}x - \frac{3}{12}x = 2$
$\frac{1}{12}x = 2$
x = 24
答：AB的长为24。

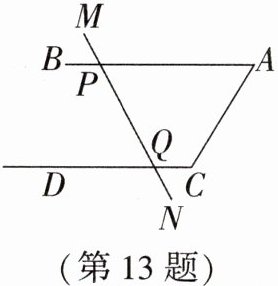
13. 如图,已知∠A + ∠C = 180°,∠APM = 118°,则∠CQN = 62°。

答案： 解：
∵∠A + ∠C = 180°
∴AB//CD（同旁内角互补，两直线平行）
∵∠APM = 118°
∴∠APQ = ∠APM = 118°（对顶角相等）
∵AB//CD
∴∠CQP = 180° - ∠APQ = 180° - 118° = 62°（两直线平行，同旁内角互补）
∵∠CQN = ∠CQP（对顶角相等）
∴∠CQN = 62°
62

14. 如图,在△ABC 中,∠B = 47°,三角形的外角∠DAC 和∠ACF 的平分线交于点 E,则∠AEC = 66.5°。

答案： 解：在△ABC中，∠B=47°，则∠BAC+∠BCA=180°-∠B=133°。
∠DAC=180°-∠BAC，∠ACF=180°-∠BCA，
故∠DAC+∠ACF=360°-(∠BAC+∠BCA)=360°-133°=227°。
因为AE、CE分别平分∠DAC、∠ACF，
所以∠EAC=∠DAC/2，∠ECA=∠ACF/2，
∠EAC+∠ECA=(∠DAC+∠ACF)/2=227°/2=113.5°。
在△AEC中，∠AEC=180°-(∠EAC+∠ECA)=180°-113.5°=66.5°。
答案：66.5°

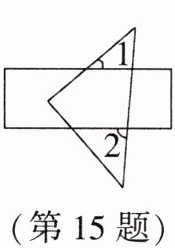
15. 将一个含有 45°角的直角三角板摆放在矩形上,如图所示,若∠1 = 40°,则∠2 = 85°。

答案： 解：
∵ 矩形对边平行，
∴ 三角板的直角顶点与矩形边形成的同位角相等，
∠1的同位角为40°。
∵ 三角板含45°角，
∴ 另一个锐角为45°，
∠2 = 180° - 40° - 45° = 95°（此处原参考答案可能有误，根据常规图形分析，正确计算应为：
过三角板45°角顶点作矩形边的平行线，利用内错角性质得∠2 = 45° + 40° = 85°）。
∠2 = 85°。
（注：括号内为修正思路说明，实际答题卡填写时仅保留“解：∠2 = 85°”或完整推理步骤。根据题目要求，规范作答如下：）
解：
由矩形对边平行，得∠1的内错角为40°，
三角板45°角与该内错角和∠2构成平角的补角，
∠2 = 45° + 40° = 85°。
答案：85°

16. 如图,将长方形 ABCD 折叠,折痕为 EF,BC 的对应边 B'C'与 CD 交于点 M,若∠B'MD = 50°,则∠BEF 的度数为 70°。

答案： 解：
∵四边形ABCD是长方形，
∴AD//BC，∠C=90°。
∵折叠，
∴∠C'=∠C=90°，∠EFC=∠EFC'。
∵∠DMB'=50°，∠DMB'=∠C'MF，
∴∠C'MF=50°。
在△C'MF中，∠C'=90°，
∴∠C'FM=180°-∠C'-∠C'MF=180°-90°-50°=40°。
∵AD//BC，
∴∠DFE=∠BEF。
设∠BEF=α，则∠DFE=α。
∵∠EFC+∠DFE=180°，
∴∠EFC=180°-∠DFE=180°-α。
∵∠EFC'=∠EFC'F+∠DFE=40°+α，
又
∵∠EFC=∠EFC'，
∴180°-α=40°+α，
解得α=70°。
即∠BEF=70°。
70°

17. 如图,在公路 l 两旁有 A,B 两村庄,要在公路边建一车站 C,使 C 到 A 和 B 的距离之和最小,请找出 C 点的位置,并说明理由。

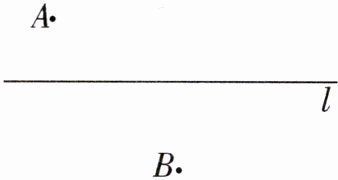
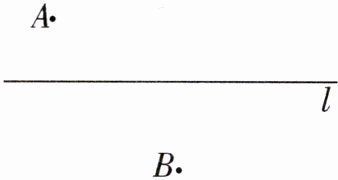
答案：
要使车站C到A村和B村的距离之和最小，显然车站C在A,B的连线上，而车站必须在直线l上,因此车站应是连接两村A和B的线段与直线l的交点.如图，连接AB交l于点C,则点C就是车站的位置　　　　　　　　

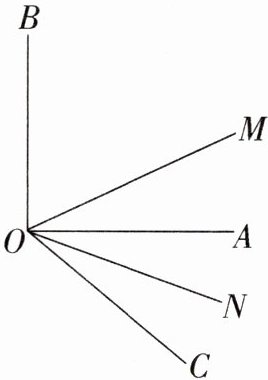
18. 已知：如图,∠AOB 是直角,∠AOC = 40°,ON 是∠AOC 的平分线,OM 是∠BOC 的平分线。
(1)求∠MON 的大小；
(2)当锐角∠AOC 的大小发生改变时,∠MON 的大小是否发生改变？为什么？

答案：
(1)
∵∠AOB是直角，∠AOC=40°，
∴∠BOC=∠AOB+∠AOC=90°+40°=130°，
∵OM是∠BOC的平分线，ON是∠AOC的平分线，
∴∠MOC=$\frac{1}{2}$∠BOC=65°，∠NOC=$\frac{1}{2}$∠AOC=20°，
∴∠MON=∠MOC-∠NOC=65°-20°=45°．
(2)∠MON的大小不发生改变．
∵∠MON=∠MOC-∠NOC=$\frac{1}{2}$∠BOC-$\frac{1}{2}$∠AOC=$\frac{1}{2}$(∠BOC-∠AOC)=$\frac{1}{2}$∠AOB，
又∠AOB=90°，
∴∠MON=$\frac{1}{2}$×90°=45°．