《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

9. 如图,$△DEF可以看作是△ABC$经过怎样的图形变换得到的? 下列结论中:①1次旋转;②2次翻折;③1次平移和1次翻折.所有正确结论的序号是①②.

答案： ①②

10. 如图,直角三角形ABC的周长为2025,在其内部有5个小直角三角形,则这5个小直角三角形周长的和是2025.

答案： 解：将5个小直角三角形的直角边分别向大直角三角形ABC的两条直角边和斜边平移，可得5个小直角三角形的直角边之和等于大直角三角形ABC的两条直角边之和，5个小直角三角形的斜边之和等于大直角三角形ABC的斜边。因此，这5个小直角三角形周长的和等于大直角三角形ABC的周长，即2025。
2025

11. 如图,$△ABC$绕点A逆时针旋转$60^{\circ }得到△ADE$,若$∠CAD= 15^{\circ }$,则$∠DAE= $45°.

答案： 解：因为△ABC绕点A逆时针旋转60°得到△ADE，所以∠BAC=∠DAE，旋转角∠BAD=60°。
又因为∠CAD=15°，所以∠BAC=∠BAD - ∠CAD=60° - 15°=45°。
因此，∠DAE=∠BAC=45°。
45°

12. 下面摆放的图案,从第2个起,每一个都是前一个按顺时针方向旋转$90^{\circ }$得到,第2025个图案与第1个至第4个中的第1个箭头方向相同.

答案： 解：观察图案可知，每4个图案为一个循环周期。
2025 ÷ 4 = 506……1，
即第2025个图案是第507个周期的第1个图案，与第1个图案箭头方向相同。
1

13. 根据光学中平面镜光线反射原理,入射光线、反射光线与平面镜所夹的角相等.如图,α,β是两面互相平行的平面镜,一束光线m通过镜面α反射后的光线为n,再通过镜面β反射后的光线为k.光线m与镜面α的夹角的度数为$x^{\circ }$,光线n与光线k的夹角的度数为$y^{\circ }$,则x与y之间的数量关系是____.

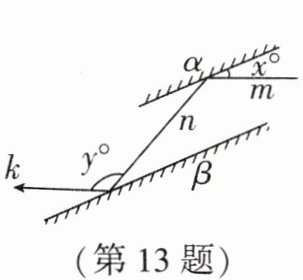
2x + y = 180

答案： 解：由平面镜反射原理，光线m与镜面α的夹角为$x^{\circ}$，则反射光线n与镜面α的夹角也为$x^{\circ}$，所以光线m与n的夹角为$180^{\circ}-2x^{\circ}$。
因为平面镜α，β互相平行，所以光线n与镜面β的夹角等于光线m与镜面α的夹角，即$x^{\circ}$，则反射光线k与镜面β的夹角也为$x^{\circ}$，光线n与k的夹角为$180^{\circ}-2x^{\circ}$。
已知光线n与k的夹角为$y^{\circ}$，故$y = 180 - 2x$，即$2x + y = 180$。
$2x + y = 180$

14. 如图,M为$∠AOB$内部的一点,P,Q分别为边OA,OB上的动点,连接PM,QM,PQ.已知$∠AOB= 60^{\circ }$,当$PM+QM+PQ$的值最小时,$∠PMQ= $____.

60°

答案： 解：作点M关于OA的对称点M₁，关于OB的对称点M₂，连接M₁M₂，分别交OA、OB于点P、Q，此时PM+QM+PQ的值最小。
连接OM₁、OM₂，由对称性质得OM₁=OM=OM₂，∠M₁OA=∠MOA，∠M₂OB=∠MOB。
∵∠AOB=60°，
∴∠M₁OM₂=2∠AOB=120°。
在△M₁OM₂中，OM₁=OM₂，
∴∠OM₁M₂=∠OM₂M₁=30°。
∵∠PMQ=180°-∠M₁PM-∠QMM₂，且∠M₁PM=∠OM₁M₂=30°，∠QMM₂=∠OM₂M₁=30°，
∴∠PMQ=180°-30°-30°=120°-60°=60°。
60°

15. 如图,直线a,b,c交于一点,且$b⊥c$,平移直线a到直线d的位置,若$∠1= 25^{\circ }$,则$∠2$的度数为____.

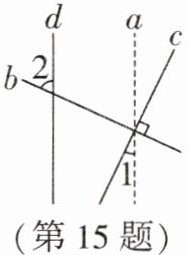
65°

答案： 解：因为直线a平移到直线d，所以a//d，
所以∠1的同位角等于∠1=25°，
又因为b⊥c，所以∠2与∠1的同位角互余，
所以∠2=90°-25°=65°。
65°

16. 如图,在一次数学活动课上,小明将一张长方形纸带进行了两次折叠,折痕分别为AB,CD,若$CD// BE,∠EBC:∠ABE= 3:5$,则$∠ADC:∠BCE= $3:7.

答案： 解：设$∠EBC = 3x$，$∠ABE = 5x$。
因为长方形纸带对边平行，折叠后$AB$为折痕，所以$∠ABE = ∠ABC = 5x$。
$∠ABC + ∠EBC = 5x + 3x = 8x$，由于纸带边缘为直线，$∠ABC + ∠EBC = 180^\circ$（平角定义），即$8x = 180^\circ$，解得$x = 22.5^\circ$。
所以$∠EBC = 3x = 67.5^\circ$，$∠ABE = 5x = 112.5^\circ$。
因为$CD// BE$，所以$∠BCD = ∠EBC = 67.5^\circ$（两直线平行，内错角相等）。
折叠后$CD$为折痕，所以$∠ADC = ∠BCD = 67.5^\circ$（折叠性质）。
$∠BCE = 180^\circ - ∠BCD = 180^\circ - 67.5^\circ = 112.5^\circ$（平角定义）。
则$∠ADC:∠BCE = 67.5^\circ:112.5^\circ = 3:7$。
$3:7$

17. (10分)如图,方格纸中的每个小方格都是边长为1的正方形,$△ABC$的顶点均在格点上.

(1)画出$△ABC$向左平移3个单位所得到的$△A_{1}B_{1}C_{1}$;
(2)画出将$△ABC$绕点O按顺时针方向旋转$90^{\circ }后所得的△A_{2}B_{2}C_{2}$;
(3)画出$△ABC$关于直线OA成轴对称的图形$△A_{3}B_{3}C_{3}$;
(4)观察所有的三角形,除了(3)中的两个三角形成轴对称外,是否还有其他成轴对称的图形? 若有,请画出它们的对称轴.

答案：

(1)如图，$\triangle A_{1}B_{1}C_{1}$即为所求.
(2)如图，$\triangle A_{2}B_{2}C_{2}$即为所求.
(3)如图，$\triangle A_{3}B_{3}C_{3}$即为所求.
(4)如图，$\triangle A_{3}B_{3}C_{3}$与$\triangle A_{2}B_{2}C_{2}$关于直线$l$对称.