第1页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 一个鸡蛋约重 (
A.1g
B.40g
C.200g
D.1kg
B
)A.1g
B.40g
C.200g
D.1kg
答案:
B
2. 标准足球场是一个长方形,其长为105米,宽为68米,它的面积的万分之一大约有(
A.一只手掌心大
B.一本数学课本大
C.一张教师讲台大
D.一个教室大
C
)A.一只手掌心大
B.一本数学课本大
C.一张教师讲台大
D.一个教室大
答案:
解:105×68 = 7140(平方米)
7140÷10000 = 0.714(平方米)
0.714平方米大约为一张教师讲台大。
答案:C
7140÷10000 = 0.714(平方米)
0.714平方米大约为一张教师讲台大。
答案:C
3. 若把面值为1元的纸币换成面值为1角或5角的硬币,则换法的种数为 (
A.4
B.3
C.2
D.1
B
)A.4
B.3
C.2
D.1
答案:
设1角硬币有x枚,5角硬币有y枚。
1元=10角,可得方程:x + 5y = 10。
y为非负整数,可能取值:
- 当y=0时,x=10;
- 当y=1时,x=5;
- 当y=2时,x=0。
共3种换法。
答案:B
1元=10角,可得方程:x + 5y = 10。
y为非负整数,可能取值:
- 当y=0时,x=10;
- 当y=1时,x=5;
- 当y=2时,x=0。
共3种换法。
答案:B
4. 在本学期,如果我们每天(星期六、星期天除外)上一节数学课,每节课45min,以18周计算,我们本学期上数学课的总时间折算成天,大约为 (
A.3天
B.6天
C.9天
D.10天以上
A
)A.3天
B.6天
C.9天
D.10天以上
答案:
解:
1. 每周上课天数:5天(星期六、星期天除外)
2. 18周上课总节数:$18 × 5 = 90$(节)
3. 总分钟数:$90 × 45 = 4050$(分钟)
4. 折算成天:$4050 ÷ (24 × 60) = 4050 ÷ 1440 \approx 2.8125$(天)
5. 结果约为3天
答案:A
1. 每周上课天数:5天(星期六、星期天除外)
2. 18周上课总节数:$18 × 5 = 90$(节)
3. 总分钟数:$90 × 45 = 4050$(分钟)
4. 折算成天:$4050 ÷ (24 × 60) = 4050 ÷ 1440 \approx 2.8125$(天)
5. 结果约为3天
答案:A
5. 把一张长方形纸片按如图①、图②的方式从右向左连续对折两次后得到图③,再在图③中挖去一个如图所示的三角形小孔,则全部展开后得到的图形是 (
C
)
答案:
C
6. 如图是某月的月历,竖着取连续的三个数,它们的和可能是 (
A.21
B.34
C.72
D.78
C
)A.21
B.34
C.72
D.78
答案:
解:设中间的数为$x$,则上面的数为$x - 7$,下面的数为$x + 7$。
三个数的和为:$(x - 7) + x + (x + 7) = 3x$,即和是$3$的倍数。
选项中$21$、$72$、$78$是$3$的倍数。
若和为$21$,则$3x = 21$,$x = 7$,上面的数为$0$,不符合实际。
若和为$72$,则$3x = 72$,$x = 24$,上面的数为$17$,下面的数为$31$,均在月历中。
若和为$78$,则$3x = 78$,$x = 26$,下面的数为$33$,月历中无$33$,不符合实际。
综上,和可能是$72$。
答案:C
三个数的和为:$(x - 7) + x + (x + 7) = 3x$,即和是$3$的倍数。
选项中$21$、$72$、$78$是$3$的倍数。
若和为$21$,则$3x = 21$,$x = 7$,上面的数为$0$,不符合实际。
若和为$72$,则$3x = 72$,$x = 24$,上面的数为$17$,下面的数为$31$,均在月历中。
若和为$78$,则$3x = 78$,$x = 26$,下面的数为$33$,月历中无$33$,不符合实际。
综上,和可能是$72$。
答案:C
7. 填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值是 (
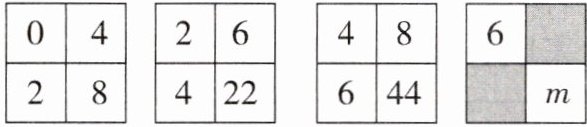
A.38
B.52
C.66
D.74
D
)
A.38
B.52
C.66
D.74
答案:
解:
观察前三个正方形数字规律:
左上角:0,2,4,6(依次+2)
右上角:4,6,8,10(依次+2)
左下角:2,4,6,8(依次+2)
右下角规律:
第一个:$2×4 - 0 = 8$
第二个:$4×6 - 2 = 22$
第三个:$6×8 - 4 = 44$
故第四个右下角 $m = 8×10 - 6 = 74$
答案:D
观察前三个正方形数字规律:
左上角:0,2,4,6(依次+2)
右上角:4,6,8,10(依次+2)
左下角:2,4,6,8(依次+2)
右下角规律:
第一个:$2×4 - 0 = 8$
第二个:$4×6 - 2 = 22$
第三个:$6×8 - 4 = 44$
故第四个右下角 $m = 8×10 - 6 = 74$
答案:D
8. 用火柴棒按如图的方式搭图形,按照这种方式搭下去,搭第8个图形需要的火柴棒的根数是 (
A.48
B.50
C.52
D.54
D
)A.48
B.50
C.52
D.54
答案:
D 提示:由图可得规律:搭第n个图形需要火柴棒的根数为$12 + 6×(n - 1) = 6n + 6$。
9. 身份证号码告诉我们很多信息,某人的身份证号码是660503196704010012,其中66,05,03是此人所属的省(直辖市、自治区)、市、县(县级市、区)的编码,1967,04,01是此人的出生年、月、日,001是顺序码,2为校验码. 若某人的身份证号码为32062119560218791X,则此人出生于
1956
年2
月18
日.
答案:
根据身份证号码编码规则,第7-14位表示出生年、月、日。该身份证号码32062119560218791X中,第7-10位为1956(出生年),第11-12位为02(出生月),第13-14位为18(出生日)。
1956 2 18
1956 2 18
查看更多完整答案,请扫码查看


