《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. 绝对值等于2的数有 (C)
A.2
B.-2
C.±2
D.0或2

答案： 解：绝对值等于2的数，即满足|x|=2的数x。
因为|2|=2，|-2|=2，所以x=±2。
答案：C

2. 在$-\frac {22}{7},π,0,0.33,0.\dot {6}\dot {8},0.3030030003…$这六个数中,有理数的个数为 (D)
A.1
B.2
C.3
D.4

答案： 解：有理数是整数和分数的统称，有限小数和无限循环小数也属于有理数。
- $-\frac{22}{7}$是分数，属于有理数；
- $π$是无限不循环小数，不属于有理数；
- $0$是整数，属于有理数；
- $0.33$是有限小数，属于有理数；
- $0.\dot{6}\dot{8}$是无限循环小数，属于有理数；
- $0.3030030003…$是无限不循环小数，不属于有理数。
综上，有理数有$-\frac{22}{7},0,0.33,0.\dot{6}\dot{8}$，共4个。
答案：D

3. 世界文化遗产长城总长约为6700000m,若将6700000用科学记数法表示为$6.7×10^{n}$(n是正整数),则n的值为 (B)
A.5
B.6
C.7
D.8

答案： 科学记数法的表示形式为$a×10^{n}$，其中$1\leq\vert a\vert＜10$，$n$为整数。确定$n$的值时，要看把原数变成$a$时，小数点移动了多少位，$n$的值与小数点移动的位数相同。当原数绝对值$\gt1$时，$n$是正数；当原数绝对值$\lt1$时，$n$是负数。
将$6700000$转变为$6.7$，小数点向左移动了$6$位，所以$n = 6$。
答案：B

4. 下列说法正确的是 (A)
A.最小的正整数是1
B.一个数的相反数一定比它本身小
C.绝对值等于它本身的数一定是正数
D.0没有倒数也没有相反数

答案： A. 最小的正整数是1，正确。
B. 负数的相反数比它本身大，0的相反数等于它本身，错误。
C. 绝对值等于它本身的数是正数和0，错误。
D. 0没有倒数，但0的相反数是0，错误。
结论：A

5. 若有理数a,b在数轴上的对应点的位置如图所示,则下列结论中错误的是 (D)
A.$ab＜0$
B.$a＜0＜b$
C.$a-(-b)＜0$
D.$b-a＜0$

答案： 由数轴可知：$a ＜ 0 ＜ b$，且$|a| ＞ |b|$。
A. $a$为负，$b$为正，$ab ＜ 0$，正确。
B. 由数轴直接可得$a ＜ 0 ＜ b$，正确。
C. $a - (-b) = a + b$，$a$绝对值大于$b$，$a + b ＜ 0$，正确。
D. $b - a = b + (-a)$，$-a$为正且$|a| ＞ |b|$，$b - a ＞ 0$，错误。
结论：错误的是D。
D

6. 下列运算中,不正确的是 (D)
A.$-15+5= -10$
B.$3\frac {4}{7}×(-3.14)-6\frac {3}{7}×3.14= -31.4$
C.$3\frac {3}{4}-(+3.75)= 0$
D.$-9÷(-3)^{2}= 1$

答案： 解：
A. $-15 + 5 = -10$，正确。
B. $3\frac{4}{7}×(-3.14) - 6\frac{3}{7}×3.14 = -3.14×(3\frac{4}{7} + 6\frac{3}{7}) = -3.14×10 = -31.4$，正确。
C. $3\frac{3}{4} - (+3.75) = 3.75 - 3.75 = 0$，正确。
D. $-9÷(-3)^2 = -9÷9 = -1 ≠ 1$，不正确。
答案：D

7. 一个数a在数轴上表示的点是A,当点A在数轴上向左平移3个单位后是点B,点A与点B表示的数互为相反数,则数a是 (C)
A.-3
B.-1.5
C.1.5
D.3

答案： 解：点A表示的数是a，向左平移3个单位后点B表示的数是a-3。
因为点A与点B表示的数互为相反数，所以a + (a - 3) = 0。
2a - 3 = 0
2a = 3
a = 1.5
答案：C

8. 为了求$1+2+2^{2}+2^{3}+…+2^{2016}$的值,可令$S= 1+2+2^{2}+2^{3}+…+2^{2016}$,则$2S= 2+2^{2}+2^{3}+2^{4}+…+2^{2017}$,因此$2S-S= 2^{2017}-1$,所以$1+2+2^{2}+2^{3}+…+2^{2016}= 2^{2017}-1$.仿照以上推理,计算:$1+5+5^{2}+5^{3}+…+5^{2025}$的值是 (C)
A.$5^{2025}-1$
B.$5^{2026}-1$
C.$\frac {5^{2026}-1}{4}$
D.$\frac {5^{2025}-1}{4}$

答案： 解：令$S = 1 + 5 + 5^{2} + 5^{3} + \ldots + 5^{2025}$，
则$5S = 5 + 5^{2} + 5^{3} + 5^{4} + \ldots + 5^{2026}$，
$5S - S = (5 + 5^{2} + 5^{3} + 5^{4} + \ldots + 5^{2026}) - (1 + 5 + 5^{2} + 5^{3} + \ldots + 5^{2025})$，
$4S = 5^{2026} - 1$，
$S = \frac{5^{2026} - 1}{4}$。
答案：C

9. 若气温为零上10℃记作+10℃,则-3℃表示气温为零下$3^{\circ}C$.

答案： 零下$3^{\circ}C$

10. $-2^{2}÷(-\frac {1}{4})=$16.

答案： 解：$-2^{2}÷(-\frac{1}{4})$
$=-4÷(-\frac{1}{4})$
$=-4×(-4)$
$=16$

11. 如果$|-a|= -(-4)$,那么$a= $$\pm4$.

答案： 解：因为$|-a| = -(-4)$，所以$|-a| = 4$。
又因为$|-a| = |a|$，所以$|a| = 4$。
则$a = \pm4$。
答案：$\pm4$

12. 在数轴上点A表示的数为-5,点B表示的数为2,则A,B两点之间的距离为7.

答案： 解：在数轴上，两点之间的距离等于这两点所表示的数的差的绝对值。
点A表示的数为-5，点B表示的数为2，
则A，B两点之间的距离为|2 - (-5)| = |2 + 5| = 7。
故答案为：7。

13. 比$-3\frac {1}{2}大而比2\frac {1}{3}$小的所有整数的和为-3.

答案： 比$-3\frac{1}{2}$大而比$2\frac{1}{3}$小的整数有：$-3$，$-2$，$-1$，$0$，$1$，$2$。
它们的和为：$-3 + (-2) + (-1) + 0 + 1 + 2$
$=(-3 - 2 - 1) + (0 + 1 + 2)$
$=-6 + 3$
$=-3$
$-3$

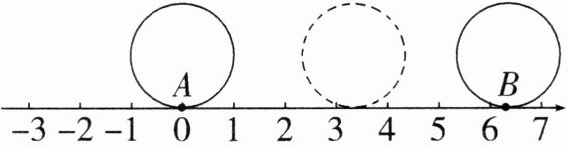
14. 如图,半径为1个单位长度的圆从原点(0)处沿数轴向右滚动一周,圆上的一点A(滚动前与原点重合)由原点到达点B,则AB的长度就等于圆的周长,所以数轴上点B代表的数是$2\pi$.

答案： 周长 $2\pi$