《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. 两条相交直线与另外一条直线在同一平面内,它们的交点个数是(D)
A.1
B.2
C.3 或 2
D.1 或 2 或 3

答案： 解：分三种情况：
1. 第三条直线过两条相交直线的交点，此时交点个数为1；
2. 第三条直线与两条相交直线中的一条平行，与另一条相交，此时交点个数为2；
3. 第三条直线与两条相交直线都相交且不过它们的交点，此时交点个数为3。
综上，交点个数是1或2或3。
答案：D

2. 沿圆柱体上底面直径截去一部分的物体如图所示,它的俯视图是(D)

答案： D

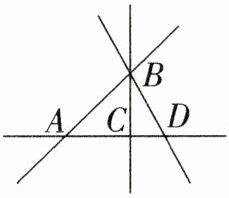
3. 如图,观察图形,下列说法中正确的个数是(B)
①直线 BA 和直线 AB 是同一条直线；②射线 AC 和射线 AD 是同一条射线；③AB + BD ＞ AD；④三条直线两两相交时,一定有三个交点。

A.1
B.2
C.3
D.4

答案： 解：①直线 BA 和直线 AB 是同一条直线，正确；
②射线 AC 和射线 AD 端点相同、方向不同，不是同一条射线，错误；
③在△ABD中，AB + BD ＞ AD（三角形两边之和大于第三边），正确；
④三条直线两两相交时，可能有1个交点（交于一点）或3个交点，错误。
正确的个数是2个。
答案：B

4. 一个多边形截去一个角后,形成的另一个多边形的内角和为 720°,那么原多边形的边数为(D)
A.5
B.5 或 6
C.5 或 7
D.5 或 6 或 7

答案： D　提示:多边形截去一个角后边数可能增加1或不变或减少1.

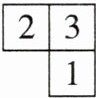
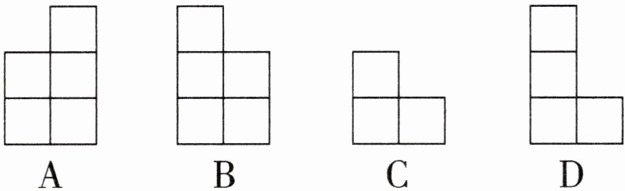
5. 如图是由几个小正方体所搭成的几何体的俯视图,小正方形中的数字表示该位置小正方体的个数,则该几何体的主视图是(A)

答案： 解：根据俯视图及小正方形中的数字，主视图有3列，从左到右每列小正方形数目分别为2，3，1。因此，该几何体的主视图是选项A。
答案：A

6. 如图是一个无盖正方体盒子,盒底标有一个字母 m,现沿箭头所指方向将盒子剪开,则展开后的图形是(A)

答案： 解：根据无盖正方体沿箭头方向剪开的特征，展开后盒底字母m的位置及相邻面关系符合选项A的图形。
答案：A

7. 如图,将五边形 ABCDE 折叠,折痕为 AF,点 E,D 分别落在点 E',D'处。已知∠AFC = 82°,则∠CFD'等于(B)
A.18°
B.16°
C.15°
D.10°

答案： 解：由折叠性质得∠AFD=∠AFD'。
∵∠AFC=82°，∠AFC+∠AFD=180°，
∴∠AFD=180°-82°=98°，
∴∠AFD'=98°，
∴∠CFD'=∠AFD'-∠AFC=98°-82°=16°。
答案：B

8. 如图,已知 AB // CD,∠ABE 与∠CDE 的平分线相交于点 F,若∠F = 125°,则∠E 的度数为(A)
A.110°
B.120°
C.115°
D.105°

答案： 解：延长BF交CD于点G。
∵AB//CD，
∴∠ABF=∠BGD。
∵BF平分∠ABE，DF平分∠CDE，
设∠ABF=∠FBE=x，∠CDF=∠FDE=y，
则∠BGD=x，∠BFD=125°。
在△DFG中，∠DGF=180°-∠BFD-∠GDF=180°-125°-y=55°-y，
又∠DGF=∠BGD=x，
∴x=55°-y，即x+y=55°。
在四边形BEDG中，∠E=360°-∠BGD-∠GDE-∠BED（此处修正为：在四边形BEDG中，∠E=360°-∠BGD-∠GDE-∠BFD所在三角形的补角，正确应为：∠E=360°-2x-2y-∠BGD的邻补角，简化后）
∠E=360°-2(x+y)-180°=360°-2×55°-180°=110°。
答案：A