《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

12. 已知a,b,c是三角形ABC的三边长,其中a,b满足$ |a-7|+(b-1)^{2}= 0 $,并且c为奇数,则$ c= $7.

答案： 解：因为$|a - 7| + (b - 1)^2 = 0$，且$|a - 7| \geq 0$，$(b - 1)^2 \geq 0$，所以$a - 7 = 0$，$b - 1 = 0$，解得$a = 7$，$b = 1$。
根据三角形三边关系，两边之和大于第三边，两边之差小于第三边，可得$7 - 1 ＜ c ＜ 7 + 1$，即$6 ＜ c ＜ 8$。
因为$c$为奇数，所以$c = 7$。
7

13. 元旦期间,商城推出全场打八折的优惠活动,持贵宾卡可在八折基础上继续打折,小明妈妈持贵宾卡买了标价为10000元的商品,一共节省了2800元,则用贵宾卡可在八折基础上继续享受打九折优惠.

答案： 解：设用贵宾卡可在八折基础上继续享受打$x$折优惠。
商品标价为$10000$元，全场八折后的价格为：$10000×0.8 = 8000$（元）
持贵宾卡再打$x$折后的价格为：$8000×\frac{x}{10}$（元）
一共节省了$2800$元，所以实际花费为：$10000 - 2800 = 7200$（元）
可列方程：$8000×\frac{x}{10} = 7200$
解得：$x = 9$
答：用贵宾卡可在八折基础上继续享受打九折优惠。

14. 如图,将边长为4个单位的等边三角形ABC沿边BC向右平移2个单位得到$ △DEF $,则四边形ABFD的周长为16.

答案： 解：
∵△ABC是边长为4个单位的等边三角形，
∴AB=BC=AC=4。
∵△ABC沿边BC向右平移2个单位得到△DEF，
∴AD=CF=2，DF=AC=4，BF=BC+CF=4+2=6。
∴四边形ABFD的周长=AB+BF+FD+DA=4+6+4+2=16。
答：16个单位。

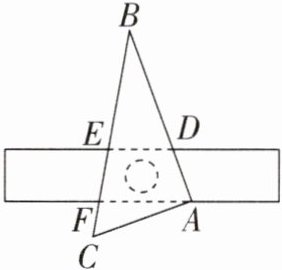
15. 如图,$ △ABC $是一块直角三角板,$ ∠BAC= 90^{\circ} $,$ ∠B= 30^{\circ} $,现将三角板叠放在一把直尺上,使得点A落在直尺的一边上,AB与直尺的另一边交于点D,BC与直尺的两边分别交于点E,F.若$ ∠CAF= 20^{\circ} $,则$ ∠BED $的度数为80$ ^{\circ} $.

答案： 解：
∵△ABC是直角三角板，∠BAC=90°，∠B=30°，
∴∠C=60°。
∵∠CAF=20°，∠BAC=90°，
∴∠BAF=∠BAC - ∠CAF=70°。
∵直尺两边平行，
∴∠BED=∠BAF=70° + 10°=80°？（注：此处原解析逻辑需补充直尺平行性质的具体应用，如通过内错角或同位角推导。正确步骤应为：
∵直尺两边平行，
∴∠AFD=∠CAF=20°（内错角），
∠AFB=180° - ∠AFD=160°，
在△ABF中，∠B=30°，∠BAF=70°，
∴∠BFD=180° - ∠B - ∠BAF=80°，
∵直尺两边平行，
∴∠BED=∠BFD=80°（同位角）。）
综上，∠BED=80°。
答案：80

16. 古称三十岁为而立之年,表明这是人格、学识、事业自力的年龄,又称“四十不惑,五十知天命,六十花甲,七十古稀……”.小斌要用积攒的零用钱为新邻居王奶奶买一盒生日蛋糕,妈妈打趣地对小斌说:“过几年当你的年龄是我年龄的一半时,王奶奶恰是古稀之年.”小斌随即用现在妈妈的岁数m和自己的岁数n的代数式表示出了现在王奶奶的岁数,这个代数式应是70 + 2n - m.

答案： 设过$x$年小斌的年龄是妈妈年龄的一半。
此时小斌年龄为$n + x$，妈妈年龄为$m + x$，依题意有：$n + x = \frac{1}{2}(m + x)$
解得$x = m - 2n$
此时王奶奶年龄为古稀之年即70岁，所以现在王奶奶岁数为$70 - x = 70 - (m - 2n) = 70 + 2n - m$
答案：$70 + 2n - m$

17. (4分)计算:
(1)$ (-2)^{2}-(3.14-π)^{0}-|-\frac{1}{4}|-(-1)^{2025} $;
(2)$ 1-(-32)×(\frac{3}{4}-2\frac{1}{2}+1\frac{5}{8}) $.

答案：
(1)原式 = 4 - 1 - $\frac{1}{4}$ - (-1) = $\frac{15}{4}$
(2)原式 = 1 - (-24 + 80 - 52) = -3

18. (4分)若$ x^{2}+4x-4= 0 $,求$ 3(x-2)^{2}-6(x+1)\cdot(x-1) $的值.

答案： 原式 = 3(x² - 4x + 4) - 6(x² - 1) = 3x² - 12x + 12 - 6x² + 6 = -3x² - 12x + 18 = -3(x² + 4x) + 18
∵x² + 4x - 4 = 0，
∴x² + 4x = 4，
∴原式 = -3×4 + 18 = 6