《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

9. 已知 $a$、$b$、$c$ 是三角形的三边长,化简：$\vert a - b - c\vert+\vert b - c + a\vert-\vert c - b - a\vert$。若 $a = 5$,$b = 4$,$c = 3$,求这个式子的值。

答案： 解：
∵a、b、c是三角形的三边长，
∴a+b＞c，b+c＞a，a+c＞b，
∴a - b - c＜0，b - c + a＞0，c - b - a＜0，
∴|a - b - c| + |b - c + a| - |c - b - a|
= -(a - b - c) + (b - c + a) - [-(c - b - a)]
= -a + b + c + b - c + a + c - b - a
= -a + b + c。
当a=5，b=4，c=3时，
原式= -5 + 4 + 3 = 2。

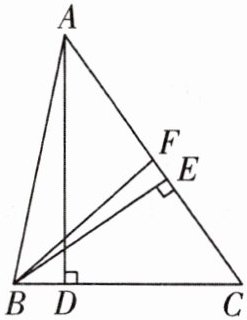
10. 如图,在 $\triangle ABC$ 中,$AC = 8$,$BC = 6$,$AD\perp BC$ 于 $D$,$AD = 6.5$,$BE\perp AC$ 于 $E$,$BF$ 是 $AC$ 边上的中线。
(1)求 $S_{\triangle ABC}$ 及 $S_{\triangle ABF}$；
(2)求 $BE$ 的长。

答案：
(1)$S_{\triangle ABC}=\frac{1}{2}BC× AD=\frac{1}{2}× 6× 6.5=\frac{39}{2}$。$\because BF$是$AC$边上的中线，$\therefore AF = FC$。$\therefore S_{\triangle ABF}=\frac{1}{2}AF× BE=\frac{1}{2}×(\frac{1}{2}AC× BE)=\frac{1}{2}S_{\triangle ABC}=\frac{1}{2}×\frac{39}{2}=\frac{39}{4}$。
(2)$\because S_{\triangle ABC}=\frac{1}{2}AC× BE$，$S_{\triangle ABC}=\frac{1}{2}BC× AD$，$\therefore AC× BE = BC× AD$，$\therefore BE=\frac{6× 6.5}{8}=\frac{39}{8}$。

11. 【发现与探究】三角形的重心
三角形三条中线的交点叫三角形的重心。重心是个物理名词。从效果上看,我们可以认为物体所受重力的合力集中于一点,这一点叫物体的重心。图①中,如果取一块均匀的三角形纸板,用一根细线绳从重心 $O$ 处将三角形提起来,纸板就会处于水平状态。为什么会平衡呢？希望你经过下面的探索过程能得到答案。图②中,$AD$ 是 $\triangle ABC$ 的中线,$\triangle ACD$ 与 $\triangle ABD$ 等底等高,面积相等,记作 $S_{\triangle ACD}= S_{\triangle ABD}$。图③中,若 $\triangle ABC$ 三条中线 $AD$、$BE$、$CF$ 交于点 $G$,则 $GD$ 是 $\triangle GBC$ 的中线,利用上述结论可得 $S_{\triangle GCD}= S_{\triangle GBD}$,同理 $S_{\triangle GBF}= S_{\triangle GAF}$,$S_{\triangle GAE}= S_{\triangle GCE}$。
(1)图③中,若设 $S_{\triangle GCD}= x$,$S_{\triangle GBF}= y$,$S_{\triangle GAE}= z$,猜想 $x$、$y$、$z$ 之间的数量关系,并证明你的猜想；
$x = y = z$。证明：由题意可知$S_{\triangle GCD}=S_{\triangle GBD}=x$，$S_{\triangle GBF}=S_{\triangle AGF}=y$，$S_{\triangle GAE}=S_{\triangle GCE}=z$。$\because S_{\triangle ABD}=S_{\triangle ACD}$，$\therefore 2y + x = 2z + x$，$\therefore y = z$。$\because S_{\triangle CBE}=S_{\triangle ABE}$，$\therefore 2x + z = 2y + z$，$\therefore x = y$，$\therefore x = y = z$。
(2)由(1)可知被三条中线分成的六个三角形面积______,如果 $\triangle ABC$ 面积为 $m$,用含有 $m$ 的式子表示 $\triangle BGC$ 的面积为______,$BG:GE= $______；
相等$\frac{1}{3}m$$2:1$
(3)图④中,$G$ 是 $\triangle ABC$ 的重心,点 $D$、$E$ 分别在 $\triangle ABC$ 的边 $AC$、$AB$ 上,$BD$、$CE$ 交于点 $G$,$BD = 12$,$CE = 9$,$BD\perp CE$,求四边形 $AEGD$ 的面积。
$\because G$是$\triangle ABC$的重心，$\therefore BG:GD = CG:GE = 2:1$。$\because BD = 12$，$CE = 9$，$\therefore BG = 8$、$CG = 6$。$\because BD\perp CE$，$\therefore S_{\triangle BGC}=\frac{1}{2}× BG× CG=\frac{1}{2}× 8× 6 = 24$，$\therefore S_{\triangle ABC}=3S_{\triangle BGC}=72$，$S_{\triangle BEC}=S_{\triangle CDG}=\frac{1}{2}S_{\triangle BGC}=12$，$\therefore S_{四边形AECD}=72 - 12 - 12 - 24 = 24$。

答案：
(1)$x = y = z$。证明：由题意可知$S_{\triangle GCD}=S_{\triangle GBD}=x$，$S_{\triangle GBF}=S_{\triangle AGF}=y$，$S_{\triangle GAE}=S_{\triangle GCE}=z$。$\because S_{\triangle ABD}=S_{\triangle ACD}$，$\therefore 2y + x = 2z + x$，$\therefore y = z$。$\because S_{\triangle CBE}=S_{\triangle ABE}$，$\therefore 2x + z = 2y + z$，$\therefore x = y$，$\therefore x = y = z$。
(2)相等 $\frac{1}{3}m$ $2:1$ 提示：由
(1)可知，被三条中线分成的六个三角形面积相等，每个小三角形的面积是大三角形面积的$\frac{1}{6}$，$\therefore \triangle BGC$的面积为$2×\frac{1}{6}m=\frac{1}{3}m$。$\because S_{\triangle BGA}=2S_{\triangle GAE}$，$\therefore 2GE = BG$，即$BG:GE = 2:1$。
(3)$\because G$是$\triangle ABC$的重心，$\therefore BG:GD = CG:GE = 2:1$。$\because BD = 12$，$CE = 9$，$\therefore BG = 8$、$CG = 6$。$\because BD\perp CE$，$\therefore S_{\triangle BGC}=\frac{1}{2}× BG× CG=\frac{1}{2}× 8× 6 = 24$，$\therefore S_{\triangle ABC}=3S_{\triangle BGC}=72$，$S_{\triangle BEC}=S_{\triangle CDG}=\frac{1}{2}S_{\triangle BGC}=12$，$\therefore S_{四边形AECD}=72 - 12 - 12 - 24 = 24$。