《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

18. (12分)已知$△ABC$中,$∠ACB= 90^{\circ },AC= BC,AB= 8,∠ABC= ∠BAC= 45^{\circ }$,点D在边AB上,$BD= a$.
(1)如图①,$△CBD$绕着点C按顺时针方向旋转,点B的对应点E落在射线CD上,点D的对应点F落在边AB上,而点E关于直线CF的对称点恰好是点A,那么DF的长度为$8 - 2a$(结果用含a的代数式表示);旋转角的度数为$30^{\circ}$;
(2)如图②,$△CBD$绕着点C按顺时针方向旋转$90^{\circ }后得到△CAG$,点B和点D的对应点分别是点A和点G,连接DG,用含a的代数式表示$S_{△ADG}$.
由旋转可得$CD = CG$，$\angle DCG = \angle ACB = 90^{\circ}$，$\angle B = \angle CAG = 45^{\circ}$，$BD = AG = a$. $\because \angle CAB = 45^{\circ}$，$\therefore \angle BAG = 90^{\circ}$. $\because AB = 8$，$\therefore AD = 8 - a$，$\therefore S_{\triangle ADG} = \frac{1}{2}a(8 - a) = -\frac{1}{2}a^{2} + 4a$.

答案：
(1)$8 - 2a$ $30^{\circ}$ 提示：$\because \triangle CBD$绕着点$C$按顺时针方向旋转，点$B$的对应点$E$落在射线$CD$上，点$D$的对应点$F$落在边$AB$上，而点$E$关于直线$CF$的对称点恰好是点$A$，$\therefore \angle BCE = \angle ECF = \angle ACF$. $\because \angle ACB = 90^{\circ}$，$\therefore \angle BCE = \angle ECF = \angle ACF = 30^{\circ}$，$\therefore$旋转角是$30^{\circ}$. $\because AC = BC$，$\angle ABC = \angle CAB = 45^{\circ}$，$\therefore \triangle ABC$是轴对称图形，由旋转可得$CD = CF$，$\therefore \triangle CDF$是轴对称图形，$\therefore BD = AF = a$. $\because AB = 8$，$\therefore DF = 8 - 2a$.
(2)由旋转可得$CD = CG$，$\angle DCG = \angle ACB = 90^{\circ}$，$\angle B = \angle CAG = 45^{\circ}$，$BD = AG = a$. $\because \angle CAB = 45^{\circ}$，$\therefore \angle BAG = 90^{\circ}$. $\because AB = 8$，$\therefore AD = 8 - a$，$\therefore S_{\triangle ADG} = \frac{1}{2}a(8 - a) = -\frac{1}{2}a^{2} + 4a$.

19. (14分)【综合实践】——折纸中的数学

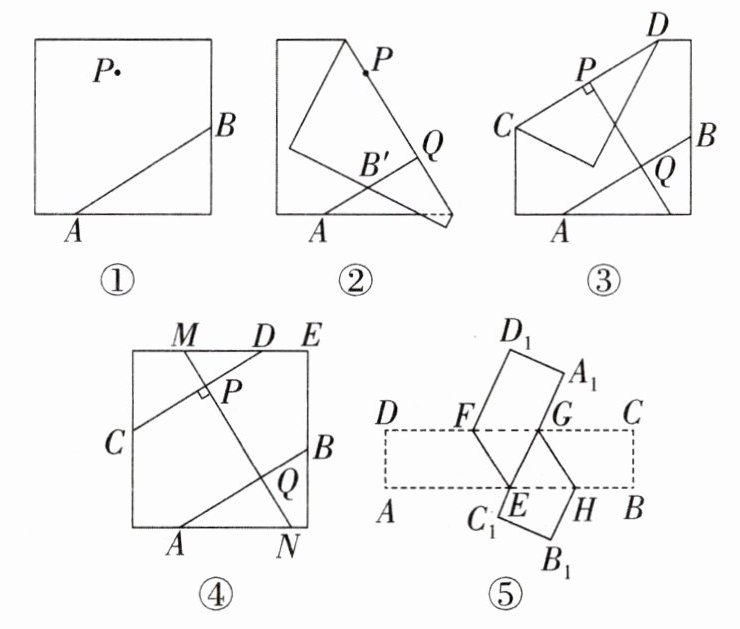
某兴趣小组在探究“过直线外一点作已知直线的平行线”的活动中,通过以下的折纸方式找符合要求的直线.如图①,在一张正方形纸片的两边上分别有A,B两点,连接AB,P是正方形纸片上一点,用折纸的方法过点P作AB的平行线的基本步骤如下:
第一步:如图②,过点P进行第一次折叠,使点B的对应点$B'$落在AB上,折痕PQ与AB互相垂直,垂足为Q,打开纸张铺平.
第二步:如图③,过点P进行第二次折叠,使折痕$CD⊥PQ$,打开纸张铺平(如图④).
(1)根据上述步骤可知,AB与CD的位置关系是____.
【联系拓广】
(2)①如图④,设直线PQ与正方形上、下两边分别交于点M,N,试探究$∠MDC与∠NAB$的数量关系,并说明理由;
②若$∠MDC= 25^{\circ }$,求$∠EBA$的度数.
【类别迁移】
(3)如图⑤,在长方形纸片ABCD中,$AB// CD$,将纸片沿EF折叠,使AD落在$A_{1}D_{1}$处,再将纸片沿GH折叠,使BC落在$B_{1}C_{1}$处,且点$A_{1},G,E,C_{1}$在同一直线上,求证:$EF// GH$.

答案：

(1)$AB // CD$ 提示：由折叠可得$PQ \perp AB$，$CD \perp PQ$，$\therefore \angle CPQ = \angle AQP = 90^{\circ}$，$\therefore \angle CPQ + \angle AQP = 180^{\circ}$，$\therefore AB // CD$.
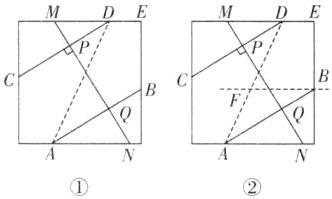
(2)①$\angle MDC = \angle NAB$. 理由如下：如图①，连接$AD$. 由纸片为正方形可知，$ME // AN$，$\therefore \angle MDA = \angle DAN$. $\because AB // CD$，$\therefore \angle CDA = \angle DAB$，$\therefore \angle MDA - \angle CDA = \angle DAN - \angle DAB$，即$\angle MDC = \angle NAB$.
②如图②，连接$AD$，过点$B$作$BF // AN$，$\therefore \angle FBA = \angle NAB = \angle MDC = 25^{\circ}$. $\because$纸片是正方形，$\therefore \angle E = 90^{\circ}$. $\because ME // AN$，$\therefore BF // ME$，$\therefore \angle FBE + \angle E = 180^{\circ}$，$\therefore \angle FBE = 180^{\circ} - \angle E = 180^{\circ} - 90^{\circ} = 90^{\circ}$，$\therefore \angle EBA = \angle FBE + \angle FBA = 90^{\circ} + 25^{\circ} = 115^{\circ}$.
　　　
(3)$\because AB // CD$，$\therefore \angle AEG = \angle CGE$. $\because$纸片沿$EF$折叠，使$AD$落在$A_{1}D_{1}$处，再将纸片沿$GH$折叠，使$BC$落在$B_{1}C_{1}$处，$\therefore \angle FEG = \frac{1}{2}\angle AEG$，$\angle EGH = \frac{1}{2}\angle CGE$，$\therefore \angle FEG = \angle EGH$，$\therefore EF // GH$.