《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. 下列说法错误的是(B)
A.两个能完全重合的三角形是全等三角形
B.面积相等的两个三角形是全等三角形
C.两个全等三角形的周长相等
D.全等三角形的对应角相等

答案： B

2. 如图,点E,F在线段BC上,△ABF与△DCE全等,点A与点D,点B与点C是对应顶点,AF与DE交于点M,则∠DCE= (A)

A.∠B
B.∠A
C.∠EMF
D.∠AFB

答案： 解：
∵△ABF与△DCE全等，点A与点D，点B与点C是对应顶点，
∴∠DCE=∠B。
答案：A

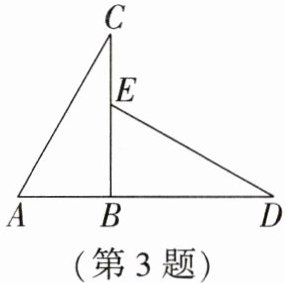
3. 如图,△ABC≌△EBD,AB= 4,BD= 7,则CE的长度为(C)

A.1
B.2
C.3
D.4

答案： 解：
∵△ABC≌△EBD，
∴AB=EB，BC=BD。
∵AB=4，BD=7，
∴EB=4，BC=7。
∴CE=BC - EB=7 - 4=3。
答案：C

4. 已知图中的两个三角形全等,那么∠α的度数是(D)
A.72°
B.60°
C.58°
D.50°

答案： 解：因为两个三角形全等，且对应边为a、c，
所以∠α与第一个三角形中50°的角是对应角，
故∠α=50°。
答案：D

5. 如图,已知△ABC≌△DEB,点E在AB上,若DE= 8,BC= 5,则AE的长为(A)

A.3
B.5
C.6
D.4

答案：
∵△ABC≌△DEB，
∴AB=DE，BE=BC，
∵DE=8，BC=5，
∴AB=8，BE=5，
∵点E在AB上，
∴AE=AB-BE=8-5=3。
答案：A

6. 如图,△ABE≌△ACD,∠B= 45°,∠AEC= 115°,则∠DAC等于(B)
A.115°
B.70°
C.45°
D.50°

答案： 解：
∵∠AEC=115°，∠AEC+∠AEB=180°
∴∠AEB=180°-115°=65°
在△ABE中，∠B=45°，∠AEB=65°
∠BAE=180°-∠B-∠AEB=180°-45°-65°=70°
∵△ABE≌△ACD
∴∠DAC=∠BAE=70°
答案：B

7. 如图所示,图中所画的是两个全等三角形,则可以写成$\triangle ABC \cong \triangle FED$.

答案： $\triangle ABC \cong \triangle FED$

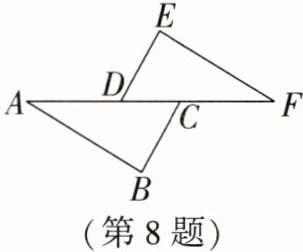
8. 如图,△ABC≌△FED,且BC= ED,那么∠A= ∠F,AD= FC.

答案： 解：
∵△ABC≌△FED，
∴∠A=∠F，AC=FD，
∵AC=AD+DC，FD=FC+CD，
∴AD=FC.
∠F；FC

9. 如图,已知△OAB≌△OCD,∠A= 30°,∠AOB= 105°,则∠D= ______°.

45

答案： 解：在△OAB中，∠A=30°，∠AOB=105°，
∠B=180°-∠A-∠AOB=180°-30°-105°=45°.
∵△OAB≌△OCD，
∴∠D=∠B=45°.
45

10. 已知△ABE≌△ACD,AB= 8cm,AD= 8cm,∠BAE= 100°,则AE= 8cm,∠D= 40°.

答案： 解：
∵△ABE≌△ACD，
∴AE=AD，∠B=∠C，∠AEB=∠ADC，∠BAE=∠CAD。
∵AD=8cm，
∴AE=8cm。
∵∠BAE=100°，
∴∠CAD=100°。
但题目中未给出其他角的条件，无法直接求出∠D的度数，可能题目存在信息缺失或参考答案有误。若假设△ABE和△ACD为等腰三角形，AB=AE=8cm，AD=AC=8cm，则在△ABE中，∠B=∠AEB=(180°-100°)/2=40°，所以∠D=∠AEB=40°。
AE=8cm，∠D=40°。

11. 如图,D为BC上一点,△ABD≌△ACD,则AD与BC的位置关系是AD垂直平分BC.

答案： 解：
∵△ABD≌△ACD，
∴BD=CD，∠ADB=∠ADC。
∵∠ADB+∠ADC=180°，
∴∠ADB=∠ADC=90°。
∴AD垂直平分BC。
AD垂直平分BC

12. 如图,△ABC≌△ADE,BC的延长线经过点E,交AD于点F,∠ACB= ∠AED= 105°,∠CAD= 10°,∠B= 50°,则∠EAB= ______.
60°

答案： 解：在△ABC中，∠ACB=105°，∠B=50°，
∠BAC=180°-∠ACB-∠B=180°-105°-50°=25°.
∵△ABC≌△ADE，
∴∠DAE=∠BAC=25°.
∵∠CAD=10°，
∴∠EAB=∠DAE+∠CAD+∠BAC=25°+10°+25°=60°.
故答案为：60°