《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

19. (7分)已知10箱苹果,以每箱15千克为标准,超过15千克的数记为正数,不足15千克的数记为负数,称重记录(单位:千克)如下:$+0.2,-0.2,+0.7,-0.3,-0.4,+0.6,0,-0.1,+0.3,-0.2$.
(1)求这10箱苹果的总质量;
(2)若每箱苹果的质量标准为$(15±0.5)$千克,则这10箱苹果中有几箱不符合标准?

答案：
(1)解：10箱苹果的标准总质量为：$15×10 = 150$（千克）
称重记录的总和为：$(+0.2)+(-0.2)+(+0.7)+(-0.3)+(-0.4)+(+0.6)+0+(-0.1)+(+0.3)+(-0.2)$
$=0.2 - 0.2 + 0.7 - 0.3 - 0.4 + 0.6 + 0 - 0.1 + 0.3 - 0.2$
$=0.6$（千克）
总质量为：$150 + 0.6 = 150.6$（千克）
(2)解：每箱苹果质量标准范围为$15 - 0.5 = 14.5$千克到$15 + 0.5 = 15.5$千克，即称重记录需满足$-0.5 \leq$记录值$\leq 0.5$。
对比记录数据：$+0.7 ＞ 0.5$，$+0.6 ＞ 0.5$，其余均在范围内。
故不符合标准的有2箱。
答：
(1)这10箱苹果的总质量为150.6千克；
(2)不符合标准的有2箱。

20. (8分)已知$|a|= 3,b^{2}= 4,ab＜0$,求$a-b$的值.

答案： 解：
∵|a|=3，
∴a=±3；
∵b²=4，
∴b=±2。
∵ab＜0，
∴当a=3时，b=-2；当a=-3时，b=2。
当a=3，b=-2时，a-b=3-(-2)=5；
当a=-3，b=2时，a-b=-3-2=-5。
综上，a-b的值为5或-5。

21. (10分)如图,已知数轴上点A表示的数为6,B是数轴上在点A左侧的一点,且A,B两点间的距离为10.动点P从点A出发,以每秒6个单位长度的速度沿数轴向左匀速运动,设运动时间为$t(t＞0)$秒.

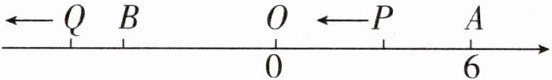
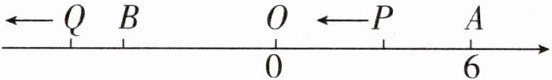
(1)数轴上点B表示的数是-4,点P表示的数是$6 - 6t$(用含t的代数式表示);
(2)动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P,Q同时出发.当点P运动多少秒时,点P与点Q相遇?
设点P运动$t$秒时与点Q相遇。
根据题意，点P运动的路程为$6t$，点Q运动的路程为$4t$，
由于点P从A出发，点Q从B出发，且A、B两点间距离为10，
当P追上Q时，$6t = 10 + 4t$，
解得$t = 5$。
答：当点P运动5秒时，点P与点Q相遇。

答案：
(1) -4；$6 - 6t$
(2) 设点P运动$t$秒时与点Q相遇。
根据题意，点P运动的路程为$6t$，点Q运动的路程为$4t$，
由于点P从A出发，点Q从B出发，且A、B两点间距离为10，
当P追上Q时，$6t = 10 + 4t$，
解得$t = 5$。
答：当点P运动5秒时，点P与点Q相遇。