《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

21. (7分)如图,直线$AB与CD相交于点O$,$OP是\angle BOC$的平分线,$OE\perp AB$,$OF\perp CD$。
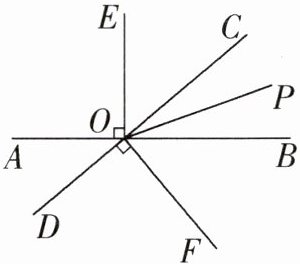
(1)图中除直角外,还有相等的角吗？请写出三对：
①$∠POC=∠POB$；
②$∠EOC=∠BOF$；
③$∠AOF=∠DOE$。
(2)如果$\angle AOD= 40^{\circ}$,
①那么根据对顶角相等,可得$\angle BOC= $40$^{\circ}$；
②求$\angle EOP$的度数。
解：$∵OP$是$∠BOC$的平分线，$∠BOC=40^{\circ}$，
$∴∠BOP=\frac{1}{2}∠BOC=20^{\circ}$．
$∵OE⊥AB$，
$∴∠EOB=90^{\circ}$．
$∴∠EOP=∠EOB-∠BOP=90^{\circ}-20^{\circ}=70^{\circ}$．

答案：
(1)①$∠POC=∠POB$；②$∠EOC=∠BOF$；③$∠AOF=∠DOE$
(2)①对顶角相等；40
②解：$∵OP$是$∠BOC$的平分线，$∠BOC=40^{\circ}$，
$∴∠BOP=\frac{1}{2}∠BOC=20^{\circ}$．
$∵OE⊥AB$，
$∴∠EOB=90^{\circ}$．
$∴∠EOP=∠EOB-∠BOP=90^{\circ}-20^{\circ}=70^{\circ}$．

22. (9分)如图,$P是线段AB$上一点,$AB= 12\ cm$,$C$,$D两点分别从P$,$B出发以1\ cm/s$,$2\ cm/s的速度沿直线AB$向左运动($C在线段AP$上,$D在线段BP$上),运动的时间为$t\ s$。

(1)当$t= 1$时,$PD= 2AC$,请求出$AP$的长；
(2)当$t= 2$时,$PD= 2AC$,请求出$AP$的长；
(3)若$C$,$D$运动到任一时刻时,总有$PD= 2AC$,请求出$AP$的长；
(4)在(3)的条件下,$Q是直线AB$上一点,且$AQ-BQ= PQ$,求$PQ$的长。

答案：
(1) 解：当$t = 1$时，$BD=2×1 = 2\space cm$，$PC = 1×1=1\space cm$，则$BD = 2PC$。
$\because PD=2AC$，$\therefore BD + PD=2(PC + AC)$，即$PB = 2AP$。
$\because AB=12\space cm$，$AB=AP + PB$，$\therefore 12=AP + 2AP=3AP$，解得$AP = 4\space cm$。
(2) 解：当$t = 2$时，$BD=2×2 = 4\space cm$，$PC=1×2 = 2\space cm$，则$BD = 2PC$。
$\because PD=2AC$，$\therefore BD + PD=2(PC + AC)$，即$PB = 2AP$。
$\because AB=12\space cm$，$AB=AP + PB$，$\therefore 12=AP + 2AP=3AP$，解得$AP = 4\space cm$。
(3) 解：运动时间为$t\space s$时，$BD=2t\space cm$，$PC=t\space cm$，则$BD = 2PC$。
$\because PD=2AC$，$\therefore BD + PD=2(PC + AC)$，即$PB = 2AP$。
$\because AB=12\space cm$，$AB=AP + PB$，$\therefore 12=AP + 2AP=3AP$，解得$AP = 4\space cm$。
(4) 解：由
(3)知$AP = 4\space cm$，则$PB=AB - AP=8\space cm$。
① 当$Q$在线段$AB$上时，$\because AQ - BQ=PQ$，$\therefore AQ=PQ + BQ$。
又$AQ=AP + PQ=4 + PQ$，$BQ=PB - PQ=8 - PQ$，
$\therefore 4 + PQ=PQ + 8 - PQ$，解得$PQ = 4\space cm$。
② 当$Q$在$AB$延长线上时，$AQ=AB + BQ$，$\because AQ - BQ=PQ$，$\therefore PQ=AB=12\space cm$。
综上，$PQ=4\space cm$或$12\space cm$。