《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. $a$的3倍与3的和不大于1,用不等式表示正确的是(B)
A.$3a + 3 ＜ 1$
B.$3a + 3 \leq 1$
C.$3a - 3 \geq 1$
D.$3a + 3 \geq 1$

答案： 解：“a的3倍”表示为3a，“与3的和”表示为3a+3，“不大于1”即小于或等于1，用不等式表示为3a+3≤1。
答案：B

2. 下列不等式中,是一元一次不等式的有(B)
①$3x - 7 ＞ 0$；②$2x + y ＞ 3$；③$2x^{2} - x ＞ 2x^{2} - 1$；④$\frac{3}{x} + 1 ＜ 7$。
A.1个
B.2个
C.3个
D.4个

答案： 解：①是一元一次不等式；
②含有两个未知数，不是一元一次不等式；
③化简后为$-x＞-1$，是一元一次不等式；
④分母含有未知数，不是一元一次不等式。
是一元一次不等式的有①③，共2个。
答案：B

3. 若$a ＜ b$,则下列结论不一定成立的是(D)
A.$a - 1 ＜ b - 1$
B.$2a ＜ 2b$
C.$-\frac{a}{3} ＞ -\frac{b}{3}$
D.$a^{2} ＜ b^{2}$

答案： 解：A. 因为$a ＜ b$，两边同时减1，不等号方向不变，所以$a - 1 ＜ b - 1$，结论成立；
B. 因为$a ＜ b$，两边同时乘2，不等号方向不变，所以$2a ＜ 2b$，结论成立；
C. 因为$a ＜ b$，两边同时除以$-3$，不等号方向改变，所以$-\frac{a}{3} ＞ -\frac{b}{3}$，结论成立；
D. 当$a = -3$，$b = 1$时，$a ＜ b$，但$a^2 = 9$，$b^2 = 1$，此时$a^2 ＞ b^2$，结论不一定成立。
答案：D

4. 如果$3x + 6$是非负数,那么$x$的取值范围是(C)
A.$x \geq 6$
B.$x ＜ 3$
C.$x \geq - 2$
D.$x \leq - 2$

答案： 解：由题意得，$3x + 6 \geq 0$
$3x \geq -6$
$x \geq -2$
答案：C

5. 不等式$x - 5 ＞ 4x - 1$的最大整数解是(A)
A.$-2$
B.$-1$
C.$0$
D.$1$

答案： 解：$x - 5 ＞ 4x - 1$
移项得：$x - 4x ＞ -1 + 5$
合并同类项得：$-3x ＞ 4$
系数化为1得：$x ＜ -\frac{4}{3}$
则不等式的最大整数解是$-2$。
A

6. 不等式组$\begin{cases}x + 2 \geq 0,\frac{1}{2}x + 2 ＜ \frac{5}{2}\end{cases} $的解集在数轴上表示正确的是(D)

答案： 解：解不等式$x + 2 \geq 0$，得$x \geq -2$。
解不等式$\frac{1}{2}x + 2 ＜ \frac{5}{2}$，两边同乘2得$x + 4 ＜ 5$，解得$x ＜ 1$。
所以不等式组的解集为$-2 \leq x ＜ 1$。
在数轴上表示为：-2处为实心点向右画线，1处为空心点向左画线，两线重合部分为解集。
答案：D

7. 若关于$x的一元一次不等式组\begin{cases}x - a ＞ 0,\\1 - 2x ＞ x - 2\end{cases} $无解,则$a$的取值范围是(A)
A.$a \geq 1$
B.$a ＞ 1$
C.$a \leq - 1$
D.$a ＜ - 1$

答案： 解：解不等式$x - a ＞ 0$，得$x ＞ a$。
解不等式$1 - 2x ＞ x - 2$，移项得$-2x - x ＞ -2 - 1$，合并同类项得$-3x ＞ -3$，系数化为$1$得$x ＜ 1$。
因为不等式组无解，所以$a \geq 1$。
答案：A

8. 某学校食堂窗口销售烤肠、汉堡、可乐和盒饭四个品种的食品,每个品种的单价均为整数,其中,汉堡的单价比烤肠的单价多3元,可乐的单价比烤肠的单价高50%,盒饭的单价是汉堡单价的4倍与可乐单价的差。某日,烤肠和汉堡一共销售了120份,且烤肠的销售量大于40份,盒饭与烤肠的销售量之和不超过400份,而可乐的销售量为60份。当日这四种食品的平均售价是汉堡单价的$\frac{5}{2}$倍,则四种食品当日销售总量的最大值为( )D
A.504
B.506
C.534
D.536

答案： 解：设烤肠单价为$x$元（$x$为整数），则汉堡单价为$(x + 3)$元，可乐单价为$1.5x$元（$x$为偶数，设$x = 2k$，$k$为整数），盒饭单价为$4(x + 3)-1.5x = 2.5x + 12$元。
设烤肠销售量为$a$份（$a＞40$，$a$为整数），则汉堡销售量为$(120 - a)$份，设盒饭销售量为$b$份，销售总量为$S = a + (120 - a) + 60 + b = b + 180$。
由题意得：$\begin{cases}a + b \leq 400\\frac{ax + (120 - a)(x + 3) + 60×1.5x + b(2.5x + 12)}{S} = \frac{5}{2}(x + 3)\end{cases}$
化简第二个方程得：$b = \frac{180x - 360}{x - 8}$，结合$a + b \leq 400$，$a＞40$，$x = 2k$且$x＞8$（$x = 10$时，$b = 360$；$x = 12$时，$b = 270$；$x = 14$时，$b = 225$；...）。
当$x = 10$时，$b = 360$，$a = 400 - b = 40$（不合$a＞40$）；取$a = 41$，则$b = 359$，此时$S = 359 + 180 = 539$（不符选项），经检验$x = 10$时，$b$最大为$356$（$a = 44$），$S = 356 + 180 = 536$。
综上，销售总量最大值为$536$。
答案：D

9. 写出一个解集为$x ＞ 1$的一元一次不等式：$x - 1 ＞ 0$。

答案： $x - 1 ＞ 0$

10. 已知不等式$(a - 2)x \leq (a - 2)的解集为x \geq 1$,那么$a$的取值范围是$a ＜ 2$。

答案： 解：因为不等式$(a - 2)x \leq (a - 2)$的解集为$x \geq 1$，
所以不等号方向改变，
则$a - 2 ＜ 0$，
解得$a ＜ 2$。
$a ＜ 2$

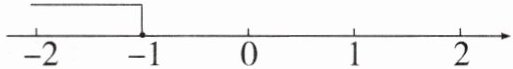
11. 关于$x的不等式2x - a \leq - 1$的解集如图所示,则$a$的值是-1。

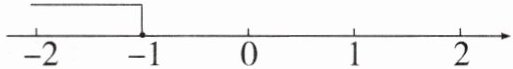
答案： 解：解不等式$2x - a \leq -1$，得$2x \leq a - 1$，$x \leq \frac{a - 1}{2}$。
由数轴可知，不等式的解集为$x \leq -1$，所以$\frac{a - 1}{2} = -1$，解得$a - 1 = -2$，$a = -1$。
$-1$

12. 不等式组$\begin{cases}x + 5 ＜ 5x + 1,\\x - m ＞ 1\end{cases} 的解集是x ＞ 1$,则$m$的取值范围是$m \leq 0$。

答案： 解：解不等式$x + 5 ＜ 5x + 1$，
移项得$x - 5x ＜ 1 - 5$，
合并同类项得$-4x ＜ -4$，
系数化为$1$得$x ＞ 1$。
解不等式$x - m ＞ 1$，
移项得$x ＞ m + 1$。
因为不等式组的解集是$x ＞ 1$，所以$m + 1 \leq 1$，
解得$m \leq 0$。
故$m$的取值范围是$m \leq 0$。

13. 若关于$x$,$y的二元一次方程组\begin{cases}2x + y = 3k - 1,\\x + 2y = - 2\end{cases} 的解满足x + y ＞ 1$,则$k$的取值范围是______。$k ＞ 2$

答案： 解：$\begin{cases}2x + y = 3k - 1,①\\x + 2y = - 2,②\end{cases}$
①+②，得$3x + 3y = 3k - 3$，
化简得$x + y = k - 1$。
因为$x + y ＞ 1$，所以$k - 1 ＞ 1$，
解得$k ＞ 2$。
$k ＞ 2$