《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

9. 三棱锥是由4个面围成的,它有4个顶点,经过每个顶点有3条棱。

答案： 4 4 3

10. 若用一个平面分别去截一个六棱柱、长方体、圆柱、圆锥,则得到的截面不可能为四边形的几何体是圆锥。

答案： 六棱柱：用平面水平或竖直截，可得到六边形、五边形、四边形等，能得到四边形。
长方体：用平面截，可得到三角形、四边形、五边形、六边形，能得到四边形。
圆柱：用平行于底面的平面截得圆形，垂直于底面的平面截得矩形（四边形），斜截可得到椭圆或四边形，能得到四边形。
圆锥：用平面截，可能得到圆形、三角形、椭圆等，截面为三角形时是轴截面，其他情况无法得到四边形。
故答案为：圆锥。

11. 将下面四个图形用纸复制下来,然后沿图形中的线折一折,把折成的立体图形的名称写出来。

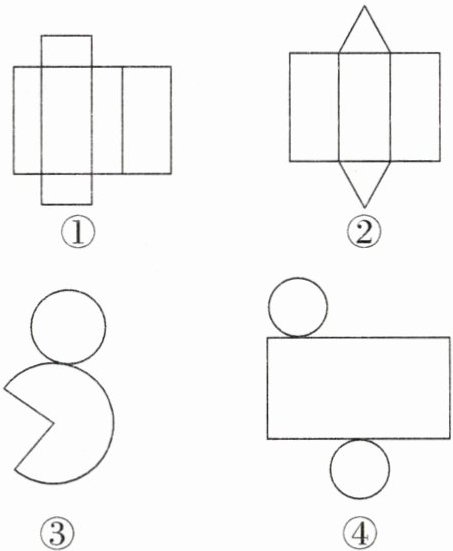
(1)图①是长方体；
(2)图②是三棱柱；
(3)图③是圆锥；
(4)图④是圆柱。

答案：
(1)长方体
(2)三棱柱
(3)圆锥
(4)圆柱

12. 如图,将图中长方形绕直线l旋转一周,得到的几何体的体积是16π。(结果保留π)

答案： 解：将长方形绕直线$l$旋转一周，得到一个底面半径为$2$，高为$4$的圆柱体。
圆柱体体积公式为$V = \pi r^2 h$，其中$r = 2$，$h = 4$。
$V=\pi×2^2×4 = \pi×4×4 = 16\pi$
$16\pi$

13. 如图是一个正方体纸盒的展开图,如果相对的面上的两个数互为相反数,那么填入正方形A,B,C中的三个数的和为-1。

答案： 解：根据正方体展开图相对面的特点，可得：
- A与-1相对，因为相对面上的数互为相反数，所以$A = -(-1) = 1$；
- B与2相对，所以$B = -2$；
- C与0相对，所以$C = -0 = 0$。
则$A + B + C = 1 + (-2) + 0 = -1$。
$-1$

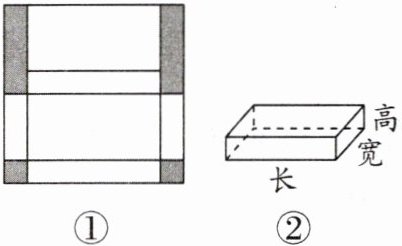
14. 一个学习小组开展了“长方体纸盒的制作”实践活动。图①是一个正方形纸板,裁掉阴影部分后将其折叠成如图②所示的长方体盒子,已知该长方体的宽是高的3倍,长比高多6 cm,则这个正方形纸板的边长为$\frac{48}{5}$cm。

答案： 解：设长方体的高为$x$cm，则宽为$3x$cm，长为$(x + 6)$cm。
由图可知，正方形纸板的边长等于长方体的长加上两个高，也等于长方体的两个宽加上两个高，即：
$x + 6 + 2x = 2×3x + 2x$
$3x + 6 = 8x$
$5x = 6$
$x = \frac{6}{5}$
正方形纸板的边长为：$x + 6 + 2x = 3x + 6 = 3×\frac{6}{5} + 6 = \frac{18}{5} + \frac{30}{5} = \frac{48}{5}$（cm）
答：这个正方形纸板的边长为$\frac{48}{5}$cm。

15. 用M,N,P,Q代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种,如图1是由M,N,P,Q中的两个图形组合而成的(组合用“&”表示),如图2所示的组合图形中表示P&Q的是②。

答案： ②

16. 用一块边长为2的正方形厚纸板ABCD,按照如图①所示的做法,将正方形ABCD沿虚线剪开,做成一套七巧板,现用它拼成一座桥,如图②所示,这座桥的阴影部分的面积是____2。

答案： 解：正方形ABCD边长为2，其面积为$2×2 = 4$。
七巧板拼成的图形面积等于原正方形面积，即桥的总面积为4。
观察图②，桥由阴影部分和空白部分组成，空白部分为两个全等的大三角形。
原正方形沿对角线剪开得到两个大三角形，每个大三角形面积为正方形面积的一半，即$4÷2 = 2$，则两个空白大三角形面积之和为2。
所以阴影部分面积 = 桥的总面积 - 空白部分面积 = $4 - 2 = 2$。
2

17. (10分)(1)如图所示,写出下列几何体的名称。

(2)将这些几何体分类,并写出分类的依据。

答案：
(1)①长方体 ②圆锥 ③六棱柱 ④球 ⑤圆柱
(2)按有无曲面分类：有曲面的几何体为②④⑤；没有曲面的几何体为①③.