《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. 已知关于$x的方程(k - 2)x^{|k| - 1} + 5 = 3k$是一元一次方程,则$k$等于(C)
A.$\pm 2$
B.$2$
C.$-2$
D.$\pm 1$

答案： 解：因为方程$(k - 2)x^{|k| - 1} + 5 = 3k$是一元一次方程，所以$|k| - 1 = 1$且$k - 2 \neq 0$。
由$|k| - 1 = 1$，得$|k| = 2$，即$k = \pm 2$。
由$k - 2 \neq 0$，得$k \neq 2$。
综上，$k = -2$。
答案：C

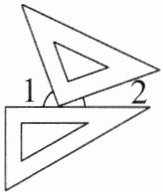
2. 一副三角板按如图方式摆放,且$\angle 1的度数比\angle 2的度数大50^{\circ}$,若设$\angle 1 = x^{\circ}$,$\angle 2 = y^{\circ}$,则可得到的方程组是( D )

A.$\begin{cases}x = y - 50,\\x + y = 180\end{cases} $
B.$\begin{cases}x = y + 50,\\x + y = 180\end{cases} $
C.$\begin{cases}x = y - 50,\\x + y = 90\end{cases} $
D.$\begin{cases}x = y + 50,\\x + y = 90\end{cases} $

答案： 解：由题意，得
$\begin{cases}x = y + 50 \\x + y = 90\end{cases}$
答案：D

3. 方程$3x + y = 7$的正整数解的个数有(B)
A.$1$个
B.$2$个
C.$3$个
D.$4$个

答案： 解：由方程$3x + y = 7$得$y = 7 - 3x$。
因为$x$、$y$为正整数，所以$x ＞ 0$，$y ＞ 0$，即：
$7 - 3x ＞ 0$，解得$x ＜ \frac{7}{3}$，所以$x$可取$1$，$2$。
当$x = 1$时，$y = 7 - 3×1 = 4$；
当$x = 2$时，$y = 7 - 3×2 = 1$。
正整数解为$\begin{cases} x=1 \\ y=4 \end{cases}$，$\begin{cases} x=2 \\ y=1 \end{cases}$，共$2$个。
B

4. 关于$x$,$y的二元一次方程组\begin{cases}x + y = 5k,\\x - y = 9k\end{cases} 的解也是二元一次方程2x + 3y = 6$的解,则$k$的值是(B)
A.$-\frac{3}{4}$
B.$\frac{3}{4}$
C.$\frac{4}{3}$
D.$-\frac{4}{3}$

答案： 解：解方程组$\begin{cases}x + y = 5k \\ x - y = 9k\end{cases}$，
两式相加得：$2x = 14k$，解得$x = 7k$，
将$x = 7k$代入$x + y = 5k$，得$7k + y = 5k$，解得$y = -2k$，
把$x = 7k$，$y = -2k$代入$2x + 3y = 6$，
得$2×7k + 3×(-2k) = 6$，
即$14k - 6k = 6$，$8k = 6$，解得$k = \frac{3}{4}$。
B

5. 一商店以每件$150$元的价格卖出两件不同的商品,其中一件盈利$25\%$,另一件亏损$25\%$,那么商店卖这两件商品总的盈亏情况是(A)
A.亏损$20$元
B.盈利$30$元
C.亏损$50$元
D.不盈不亏

答案： 解：设盈利商品的成本为$x$元，亏损商品的成本为$y$元。
盈利商品：$x(1 + 25\%) = 150$
$1.25x = 150$
$x = 120$
盈利：$150 - 120 = 30$元
亏损商品：$y (1 - 25\%) = 150$
$0.75y = 150$
$y = 200$
亏损：$200 - 150 = 50$元
总盈亏：$30 - 50 = -20$元，即亏损20元。
A

6. 小岩打算购买气球装扮学校“毕业典礼”活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同.由于会场布置需要,购买时以一束($4$个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为(B)
A.$19$元
B.$18$元
C.$16$元
D.$15$元

答案： 解：设笑脸气球单价为$x$元，爱心气球单价为$y$元。
由第一束（3笑脸+1爱心）得：$3x + y = 16$
由第二束（1笑脸+3爱心）得：$x + 3y = 20$
两式相加：$4x + 4y = 36$，即$x + y = 9$
第三束为2笑脸+2爱心，价格为$2x + 2y = 2(x + y) = 2×9 = 18$元
答案：B

7. 小明在解关于$x$,$y的二元一次方程组\begin{cases}x + \otimes y = 9,\\3x - \otimes y = 3\end{cases} $时,得到了正确结果$\begin{cases}x = \oplus,\\y = 2.\end{cases} $后来发现“$\otimes$”“$\oplus$”处被墨水污损了,则“$\otimes$”“$\oplus$”处的值分别是(B)
A.$\otimes = 2$,$\oplus = 3$
B.$\otimes = 3$,$\oplus = 3$
C.$\otimes = 2$,$\oplus = 1$
D.$\otimes = 3$,$\oplus = 4$

答案： 解：设“$\otimes$”处的值为$a$，“$\oplus$”处的值为$b$，则原方程组为：
$\begin{cases}x + ay = 9 \\3x - ay = 3\end{cases}$
已知方程组的解为$\begin{cases} x = b \\ y = 2 \end{cases}$，将其代入方程组得：
$\begin{cases}b + 2a = 9 & (1) \\3b - 2a = 3 & (2)\end{cases}$
$(1)+(2)$得：$4b = 12$，解得$b = 3$。
将$b = 3$代入$(1)$得：$3 + 2a = 9$，解得$a = 3$。
所以“$\otimes$”处的值为$3$，“$\oplus$”处的值为$3$。
答案：B

8. 如果方程组$\begin{cases}x + y = 1,\\ax + by = c\end{cases} $有唯一的一组解,那么$a$,$b$,$c$的值应当满足的条件是(B)
A.$a = 1$,$c = 1$
B.$a \neq b$
C.$a = b = 1$,$c \neq 1$
D.$a = 1$,$c \neq 1$

答案： 解：对于方程组$\begin{cases}x + y = 1\\ax + by = c\end{cases}$，将第一个方程变形为$x = 1 - y$，代入第二个方程得：$a(1 - y) + by = c$，即$(b - a)y = c - a$。要使方程组有唯一解，则系数$b - a \neq 0$，即$a \neq b$。
答案：B

9. 已知关于$x的一元一次方程a(x - 4) = -4x + 3a的解是x = 3$,则$a = $3.

答案： 解：将$x = 3$代入方程$a(x - 4) = -4x + 3a$，得
$a(3 - 4) = -4×3 + 3a$
$-a = -12 + 3a$
$-a - 3a = -12$
$-4a = -12$
$a = 3$
3

10. 已知方程组$\begin{cases}ax - by = 4,\\ax + by = 2\end{cases} 的解为\begin{cases}x = 2,\\y = 1,\end{cases} 则2a - 3b$的值为______6.

答案： 解：将$\begin{cases}x = 2\\y = 1\end{cases}$代入方程组$\begin{cases}ax - by = 4\\ax + by = 2\end{cases}$，得
$\begin{cases}2a - b = 4 \\2a + b = 2 \end{cases}$
两式相加：$4a = 6$，解得$a = \frac{3}{2}$
将$a = \frac{3}{2}$代入$2a - b = 4$，得$3 - b = 4$，解得$b = -1$
则$2a - 3b = 2×\frac{3}{2} - 3×(-1) = 3 + 3 = 6$
6