《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. 下列图案中,是轴对称图形的是 (C)

答案： C

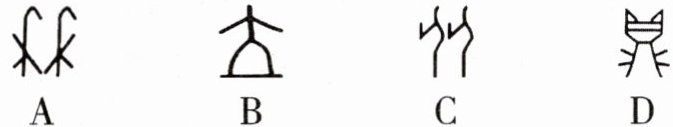
2. 甲骨文是我国的一种古代文字,是汉字的早期形式,下列甲骨文中,能用其中一部分平移得到的是 (C)

答案： C

3. 如图,$△ABC$沿BC方向平移a cm后,得到$△A'B'C'$,已知$BC= 6cm,BC'= 17cm$,则a的值为 (B)

A.10
B.11
C.12
D.13

答案： 解：由平移性质得，平移距离 $a = CC'$。
已知 $BC = 6\,\text{cm}$，$BC' = 17\,\text{cm}$，
则 $CC' = BC' - BC = 17 - 6 = 11\,\text{cm}$，
即 $a = 11$。
答案：B

4. 如图,已知$∠BAC= 70^{\circ }$,过AB边上一点O作直线OD,经测量$∠AOD= 95^{\circ }$,要使$OD// AC$,直线OD绕点O按逆时针方向至少旋转 (B)
A.$5^{\circ }$
B.$15^{\circ }$
C.$20^{\circ }$
D.$25^{\circ }$

答案： 解：要使$OD// AC$，根据两直线平行，同旁内角互补，此时$\angle AOD' + \angle BAC = 180^{\circ}$（设旋转后直线为$OD'$）。
已知$\angle BAC = 70^{\circ}$，则$\angle AOD' = 180^{\circ} - 70^{\circ} = 110^{\circ}$。
原$\angle AOD = 95^{\circ}$，所以旋转角度为$\angle AOD' - \angle AOD = 110^{\circ} - 95^{\circ} = 15^{\circ}$。
答案：B

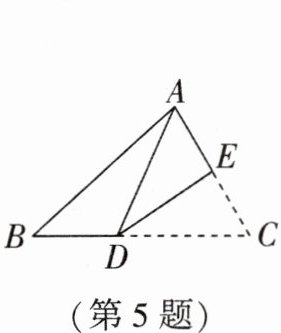
5. 如图,$△ABC$的周长为40 cm,把$△ABC$的边AC对折,使顶点C和点A重合,折痕交BC边于点D,交AC于点E,若$AE= 6cm$,则$△ABD$的周长是 (B)

A.34 cm
B.28 cm
C.25 cm
D.22 cm

答案： 解：由折叠性质得，AE=CE，AD=CD。
∵AE=6cm，
∴AC=AE+CE=12cm。
∵△ABC的周长为40cm，
∴AB+BC+AC=40cm，
∴AB+BC=40-12=28cm。
△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC=28cm。
答案：B

6. 如图,在正三角形网格中,将$△EFG绕某个点旋转得到△E'F'G'$,则能作为旋转中心的是 (C)
A.点A
B.点B
C.点C
D.点D

答案： 连接$EE'$、$FF'$、$GG'$，分别作$EE'$、$FF'$、$GG'$的垂直平分线，三条垂直平分线交于点$C$。
C

7. 如图,将直角三角形ABC沿BC方向平移4 cm,得到直角三角形DEF.已知$AB= 8cm$,$DH= 3cm$,则有下列说法:①$CH// DF$;②$∠DHA= ∠F$;③$HE= 5cm$;④图中阴影部分的面积为$26cm^{2}$.其中一定正确的是 (C)
A.①③④
B.①②
C.①②③④
D.①②④

答案： 解：①由平移性质得DF//AC，即CH//DF，正确；
②
∵CH//DF，
∴∠DHA=∠F，正确；
③由平移性质得DE=AB=8cm，HE=DE-DH=8-3=5cm，正确；
④由平移性质得BE=4cm，阴影部分面积=梯形ABEH面积=$\frac{1}{2}$×(AB+HE)×BE=$\frac{1}{2}$×(8+5)×4=26cm²，正确。
综上，①②③④均正确，答案选C。

8. 将长方形纸片ABCD按照如图所示的方式折叠两次,第一次将四边形EFCB沿EF折叠得到四边形EFGH,EH交DC于点M,第二次将四边形MHGF沿FM折叠形成四边形$MFG'H'$,若$∠EFM= \frac {1}{6}∠EFG'$,则$∠EFM$的度数为 (A)
A.$20^{\circ }$
B.$22.5^{\circ }$
C.$(\frac {180}{7})^{\circ }$
D.$30^{\circ }$

答案： A