第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
10. 若 $ x < y $,且 $ (m - 2)x > (m - 2)y $,则 $ m $ 的取值范围是
$ m < 2 $
。
答案:
解:因为 $ x < y $,且 $ (m - 2)x > (m - 2)y $,
所以不等式两边同时乘以$ (m - 2) $后,不等号方向改变,
根据不等式的性质,可得 $ m - 2 < 0 $,
解得 $ m < 2 $。
故答案为:$ m < 2 $
所以不等式两边同时乘以$ (m - 2) $后,不等号方向改变,
根据不等式的性质,可得 $ m - 2 < 0 $,
解得 $ m < 2 $。
故答案为:$ m < 2 $
11. 当
$a \geq 1$
时,关于 $ x $ 的方程 $ 4(x + 2) - 5 = 3a + 2 $ 的解不小于 $ \frac{1}{2} $。
答案:
解:解方程 $4(x + 2) - 5 = 3a + 2$,
去括号得:$4x + 8 - 5 = 3a + 2$,
化简得:$4x + 3 = 3a + 2$,
移项得:$4x = 3a + 2 - 3$,
合并同类项得:$4x = 3a - 1$,
系数化为1得:$x = \frac{3a - 1}{4}$。
因为方程的解不小于$\frac{1}{2}$,所以$\frac{3a - 1}{4} \geq \frac{1}{2}$,
两边同时乘以4得:$3a - 1 \geq 2$,
移项得:$3a \geq 3$,
解得:$a \geq 1$。
$a \geq 1$
去括号得:$4x + 8 - 5 = 3a + 2$,
化简得:$4x + 3 = 3a + 2$,
移项得:$4x = 3a + 2 - 3$,
合并同类项得:$4x = 3a - 1$,
系数化为1得:$x = \frac{3a - 1}{4}$。
因为方程的解不小于$\frac{1}{2}$,所以$\frac{3a - 1}{4} \geq \frac{1}{2}$,
两边同时乘以4得:$3a - 1 \geq 2$,
移项得:$3a \geq 3$,
解得:$a \geq 1$。
$a \geq 1$
12. 若不等式组 $ \begin{cases} 2x - b \geq 0, \\ x + a \leq 0 \end{cases} $ 的解集为 $ 3 \leq x \leq 4 $,则不等式 $ ax + b < 0 $ 的解集为
$x > \frac{3}{2}$
。
答案:
解:解不等式组$\begin{cases}2x - b \geq 0 \\ x + a \leq 0\end{cases}$,
由$2x - b \geq 0$得$x \geq \frac{b}{2}$,
由$x + a \leq 0$得$x \leq -a$。
因为不等式组的解集为$3 \leq x \leq 4$,
所以$\frac{b}{2} = 3$,$-a = 4$,
解得$b = 6$,$a = -4$。
则不等式$ax + b < 0$为$-4x + 6 < 0$,
$-4x < -6$,
$x > \frac{3}{2}$。
故答案为$x > \frac{3}{2}$。
由$2x - b \geq 0$得$x \geq \frac{b}{2}$,
由$x + a \leq 0$得$x \leq -a$。
因为不等式组的解集为$3 \leq x \leq 4$,
所以$\frac{b}{2} = 3$,$-a = 4$,
解得$b = 6$,$a = -4$。
则不等式$ax + b < 0$为$-4x + 6 < 0$,
$-4x < -6$,
$x > \frac{3}{2}$。
故答案为$x > \frac{3}{2}$。
13. 在一次“人与自然”的知识竞赛中,竞赛试题共有 25 道,每道题都给出 4 个答案,其中只有一个答案正确,要求学生把正确答案选出来,每道题选对得 4 分,不选或选错倒扣 2 分。如果一个学生在本次竞赛中的得分不低于 60 分,那么他至少选对了______道题。
19
答案:
解:设他选对了$x$道题,则不选或选错的有$(25 - x)$道题。
根据题意,得$4x - 2(25 - x) \geq 60$,
去括号,得$4x - 50 + 2x \geq 60$,
合并同类项,得$6x - 50 \geq 60$,
移项,得$6x \geq 110$,
系数化为$1$,得$x \geq \frac{55}{3} \approx 18.33$。
因为$x$为整数,所以$x$的最小值为$19$。
19
根据题意,得$4x - 2(25 - x) \geq 60$,
去括号,得$4x - 50 + 2x \geq 60$,
合并同类项,得$6x - 50 \geq 60$,
移项,得$6x \geq 110$,
系数化为$1$,得$x \geq \frac{55}{3} \approx 18.33$。
因为$x$为整数,所以$x$的最小值为$19$。
19
14. 下面是一个运算程序图,若需要经过两次运算才能输出结果 $ y $,则输入的 $ x $ 的取值范围是______。


$4 \leq x < 11$
答案:
解:第一次运算结果:$3x - 1$
因为第一次运算不输出,所以$3x - 1 < 32$,解得$x < 11$
第二次运算结果:$3(3x - 1) - 1 = 9x - 4$
因为第二次运算输出,所以$9x - 4 \geq 32$,解得$x \geq 4$
综上,$4 \leq x < 11$
$4 \leq x < 11$
因为第一次运算不输出,所以$3x - 1 < 32$,解得$x < 11$
第二次运算结果:$3(3x - 1) - 1 = 9x - 4$
因为第二次运算输出,所以$9x - 4 \geq 32$,解得$x \geq 4$
综上,$4 \leq x < 11$
$4 \leq x < 11$
15. 若不等式组 $ \begin{cases} 2x + a > 0, \\ \frac{1}{2}x > -\frac{a}{4} + 1 \end{cases} $ 的解集中的任意 $ x $,都能使不等式 $ x - 5 > 0 $ 成立,则 $ a $ 的取值范围是
$a \leq -6$
。
答案:
解:解不等式 $2x + a > 0$,得 $x > -\frac{a}{2}$。
解不等式 $\frac{1}{2}x > -\frac{a}{4} + 1$,两边同乘 2 得 $x > -\frac{a}{2} + 2$。
所以不等式组的解集为 $x > -\frac{a}{2} + 2$。
因为不等式组的解集中的任意 $x$ 都能使 $x - 5 > 0$(即 $x > 5$)成立,所以 $ -\frac{a}{2} + 2 \geq 5$。
解得 $ -\frac{a}{2} \geq 3$,即 $a \leq -6$。
$a \leq -6$
解不等式 $\frac{1}{2}x > -\frac{a}{4} + 1$,两边同乘 2 得 $x > -\frac{a}{2} + 2$。
所以不等式组的解集为 $x > -\frac{a}{2} + 2$。
因为不等式组的解集中的任意 $x$ 都能使 $x - 5 > 0$(即 $x > 5$)成立,所以 $ -\frac{a}{2} + 2 \geq 5$。
解得 $ -\frac{a}{2} \geq 3$,即 $a \leq -6$。
$a \leq -6$
16. 对于任意实数 $ m, n $,定义一种运算: $ m※n = mn - m - n + 3 $,等式的右边是通常的加减和乘法运算,例如: $ 3※5 = 3×5 - 3 - 5 + 3 = 10 $。请根据上述定义解决问题:若 $ a < 2※x < 7 $,且解集中有两个整数解,则 $ a $ 的取值范围是______
$4 ≤ a < 5$
。
答案:
解:根据定义,$2※x = 2x - 2 - x + 3 = x + 1$。
∵ $a < 2※x < 7$,
∴ $a < x + 1 < 7$,
即 $a - 1 < x < 6$。
∵ 解集中有两个整数解,
∴ 这两个整数解为 4,5,
∴ $3 ≤ a - 1 < 4$,
解得 $4 ≤ a < 5$。
$4 ≤ a < 5$
∵ $a < 2※x < 7$,
∴ $a < x + 1 < 7$,
即 $a - 1 < x < 6$。
∵ 解集中有两个整数解,
∴ 这两个整数解为 4,5,
∴ $3 ≤ a - 1 < 4$,
解得 $4 ≤ a < 5$。
$4 ≤ a < 5$
17. 解下列不等式(组),并把不等式(组)的解集在数轴上表示出来:
(1) $ 5x - 12 \leq 2(4x - 3) $;
(2) $ \frac{x + 4}{3} - \frac{3x - 1}{2} > 1 $;
(3) $ \begin{cases} 3x \geq x + 2, \\ x + 4 < 2(2x - 1) \end{cases} $;
(4) $ \begin{cases} \frac{1}{2}(x + 1) \leq 2, \\ \frac{x + 2}{2} \geq \frac{x + 3}{3} \end{cases} $。
(1) $ 5x - 12 \leq 2(4x - 3) $;
(2) $ \frac{x + 4}{3} - \frac{3x - 1}{2} > 1 $;
(3) $ \begin{cases} 3x \geq x + 2, \\ x + 4 < 2(2x - 1) \end{cases} $;
(4) $ \begin{cases} \frac{1}{2}(x + 1) \leq 2, \\ \frac{x + 2}{2} \geq \frac{x + 3}{3} \end{cases} $。
答案:
(1) 去括号, 得 5x - 12 ≤ 8x - 6,移项, 得 5x - 8x ≤ -6 + 12,合并同类项, 得 -3x ≤ 6,系数化为 1, 得 x ≥ -2.不等式的解集在数轴上表示如图所示: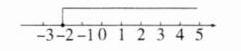
(2) 去分母, 得 2(x + 4) - 3(3x - 1) > 6,去括号, 得 2x + 8 - 9x + 3 > 6,移项, 得 2x - 9x > 6 - 8 - 3,合并同类项, 得 -7x > -5,系数化为 1, 得 x < $\frac{5}{7}.$不等式的解集在数轴上表示如图所示:
(3) $ \begin{cases} 3x ≥ x + 2, & ① \\ x + 4 < 2(2x - 1), & ② \end{cases} $解不等式①得, x ≥ 1,解不等式②得, x > 2,
∴ 该不等式组的解集为 x > 2.不等式组的解集在数轴上表示如图所示: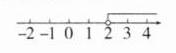
(4) $ \begin{cases} \frac{1}{2}(x + 1) ≤ 2, & ① \\ \frac{x + 2}{2} ≥ \frac{x + 3}{3}, & ② \end{cases} $解不等式①得, x ≤ 3,解不等式②得, x ≥ 0,
∴ 该不等式组的解集为 0 ≤ x ≤ 3.不等式组的解集在数轴上表示如图所示:
(1) 去括号, 得 5x - 12 ≤ 8x - 6,移项, 得 5x - 8x ≤ -6 + 12,合并同类项, 得 -3x ≤ 6,系数化为 1, 得 x ≥ -2.不等式的解集在数轴上表示如图所示:
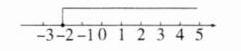
(2) 去分母, 得 2(x + 4) - 3(3x - 1) > 6,去括号, 得 2x + 8 - 9x + 3 > 6,移项, 得 2x - 9x > 6 - 8 - 3,合并同类项, 得 -7x > -5,系数化为 1, 得 x < $\frac{5}{7}.$不等式的解集在数轴上表示如图所示:

(3) $ \begin{cases} 3x ≥ x + 2, & ① \\ x + 4 < 2(2x - 1), & ② \end{cases} $解不等式①得, x ≥ 1,解不等式②得, x > 2,
∴ 该不等式组的解集为 x > 2.不等式组的解集在数轴上表示如图所示:
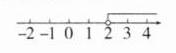
(4) $ \begin{cases} \frac{1}{2}(x + 1) ≤ 2, & ① \\ \frac{x + 2}{2} ≥ \frac{x + 3}{3}, & ② \end{cases} $解不等式①得, x ≤ 3,解不等式②得, x ≥ 0,
∴ 该不等式组的解集为 0 ≤ x ≤ 3.不等式组的解集在数轴上表示如图所示:

18. 已知 $ \begin{cases} 3x + 2y = k + 1, \\ 4x + 3y = k - 1 \end{cases} $ 的解中 $ x, y $ 同号,求整数 $ k $ 的值。
答案:
解:解方程组$\begin{cases}3x + 2y = k + 1 \\ 4x + 3y = k - 1\end{cases}$,
由$3×(3x + 2y) - 2×(4x + 3y)=3(k + 1)-2(k - 1)$,
得$9x + 6y - 8x - 6y = 3k + 3 - 2k + 2$,
解得$x = k + 5$,
将$x = k + 5$代入$3x + 2y = k + 1$,得$3(k + 5) + 2y = k + 1$,
$3k + 15 + 2y = k + 1$,$2y = -2k - 14$,解得$y = -k - 7$,
所以$\begin{cases}x = k + 5 \\ y = -k - 7\end{cases}$。
因为$x$,$y$同号,所以有两种情况:
情况一:$\begin{cases}k + 5 > 0 \\ -k - 7 > 0\end{cases}$,
解得$\begin{cases}k > -5 \\ k < -7\end{cases}$,此不等式组无解;
情况二:$\begin{cases}k + 5 < 0 \\ -k - 7 < 0\end{cases}$,
解得$\begin{cases}k < -5 \\ k > -7\end{cases}$,即$-7 < k < -5$。
因为$k$为整数,所以$k = -6$。
答:整数$k$的值为$-6$。
由$3×(3x + 2y) - 2×(4x + 3y)=3(k + 1)-2(k - 1)$,
得$9x + 6y - 8x - 6y = 3k + 3 - 2k + 2$,
解得$x = k + 5$,
将$x = k + 5$代入$3x + 2y = k + 1$,得$3(k + 5) + 2y = k + 1$,
$3k + 15 + 2y = k + 1$,$2y = -2k - 14$,解得$y = -k - 7$,
所以$\begin{cases}x = k + 5 \\ y = -k - 7\end{cases}$。
因为$x$,$y$同号,所以有两种情况:
情况一:$\begin{cases}k + 5 > 0 \\ -k - 7 > 0\end{cases}$,
解得$\begin{cases}k > -5 \\ k < -7\end{cases}$,此不等式组无解;
情况二:$\begin{cases}k + 5 < 0 \\ -k - 7 < 0\end{cases}$,
解得$\begin{cases}k < -5 \\ k > -7\end{cases}$,即$-7 < k < -5$。
因为$k$为整数,所以$k = -6$。
答:整数$k$的值为$-6$。
查看更多完整答案,请扫码查看


