《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

19. 如图,$AB // CD$,分别探讨下面四个图形中$∠APC与∠PAB$,$∠PCD$的关系,请你从所得到的关系中任选一个加以证明.

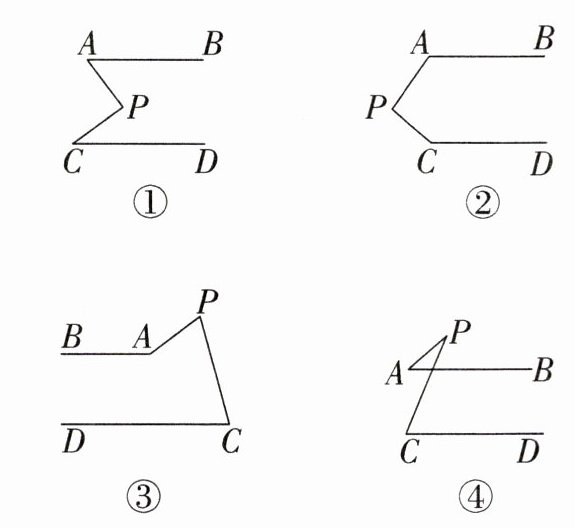
答案： ①$∠APC=∠PAB+∠PCD$。
②$∠APC+∠PAB+∠PCD=360^{\circ }$。
③$∠APC=∠PAB-∠PCD$。
④$∠APC=∠PCD-∠PAB$。
证明：选①。
过点$P$作$PF// AB$（$F$在$P$的左边）。
$\because AB// CD$，
$\therefore AB// CD// PF$。
$\therefore ∠PAB=∠APF$，$∠PCD=∠CPF$。
$\because ∠APF+∠CPF=∠APC$，
$\therefore ∠APC=∠PAB+∠PCD$。

20. 阅读下面材料：
点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为|AB|.当A,B两点中有一点在原点时,不妨设点A在原点,如图①,|AB| = |OB| = |b| = |a - b|；当A,B两点都不在原点时,Ⅰ.如图②,点A,B都在原点的右边,|AB| = |OB| - |OA| = |b| - |a| = b - a = |a - b|；Ⅱ.如图③,点A,B都在原点的左边,|AB| = |OB| - |OA| = |b| - |a| = - b - (- a) = |a - b|；Ⅲ.如图④,点A,B在原点的两边,|AB| = |OB| + |OA| = |a| + |b| = a + (- b) = |a - b|.回答下列问题：(1)数轴上表示2和5的两点之间的距离是3；数轴上表示-2和-5的两点之间的距离是3；数轴上表示1和-3的两点之间的距离是4.(2)数轴上表示x和-1的两点A和B之间的距离是|x + 1|；如果|AB| = 2,那么x为1 或 -3.(3)当代数式|x + 1| + |x - 2|取最小值时,相应的x的取值范围是-1 ≤ x ≤ 2.

答案：
(1) 3；3；4
(2) $|x + 1|$；1 或 -3
(3) $-1 \leq x \leq 2$