《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

1. 下列说法中正确的是(C)
A.棱柱的侧面可以是三角形
B.由六个大小一样的正方形所组成的图形是正方体的展开图
C.正方体的各条棱都相等
D.棱柱的各条棱都相等

答案： C

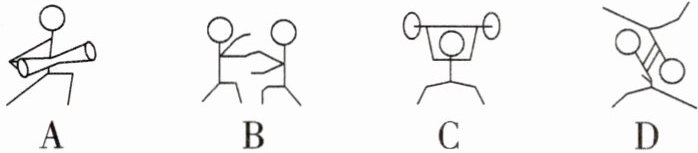
2. 下面四幅画分别是体育运动长鼓舞、武术、举重、摔跤抽象出来的简笔画,其中沿某一条直线折叠后,直线两旁的部分能够互相重合的图形是(C)

答案： 沿某一条直线折叠后，直线两旁的部分能够互相重合的图形是轴对称图形。观察各选项：
- A 图形无对称轴，不是轴对称图形；
- B 图形无对称轴，不是轴对称图形；
- C 图形沿中间竖直直线折叠，两旁部分重合，是轴对称图形；
- D 图形无对称轴，不是轴对称图形。
答案：C

3. 将如图所示的平面图形绕轴l旋转一周,可以得到的立体图形是(D)

答案： 观察平面图形，其为直角梯形，绕轴$l$（梯形的一条直角边）旋转一周。
梯形的上底较短，下底较长，绕直角边旋转时，上底旋转形成一个较小的圆面，下底旋转形成一个较大的圆面，梯形的斜边旋转形成连接两个圆面边缘的曲面。
因此，得到的立体图形是圆台，对应选项D。
答案：D

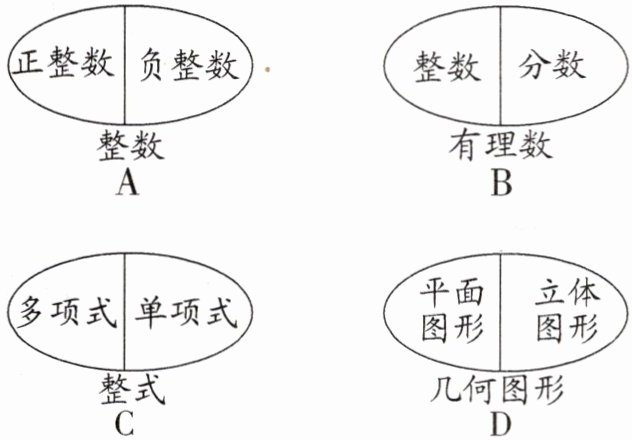
4. 小聪同学对所学的部分知识进行分类,其中分类错误的是(A)

答案： A

5. 如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是(B)
A.蓝色、绿色、黑色
B.绿色、蓝色、黑色
C.绿色、黑色、蓝色
D.蓝色、黑色、绿色

答案： 解：从第一个正方体可知，白色与黑色、黄色相邻，故白色对面不是黑、黄；从第二个正方体可知，白色与绿色、红色相邻，故白色对面不是绿、红，因此白色对面只能是蓝色。
从第一个正方体可知，黄色与白色、黑色相邻；从第三个正方体可知，黄色与蓝色、红色相邻，故黄色对面不是白、黑、蓝、红，因此黄色对面只能是绿色。
剩下红色对面只能是黑色。
综上，黄色对面是绿色，白色对面是蓝色，红色对面是黑色。答案选B。

6. 如图所示的正方体,如果把它展开,可以是下列图形中的(B)

答案： 解：通过观察正方体的相对面和相邻面特征，分析各选项展开图：
- 原正方体中，圆形面与阴影面、三角形面相邻。
- 选项A中圆形面与三角形面不相邻，不符合；
- 选项C中圆形面与三角形面不相邻，不符合；
- 选项D中阴影面与三角形面相邻位置错误，不符合；
- 选项B中各面相邻关系与原正方体一致。
答案：B

7. 如图,把一张边长为24 cm的正方形纸片的四个角各剪去一个同样大小的小正方形,然后把剩下的部分折成一个无盖的长方体盒子,当剪去的小正方形的边长从4 cm变为5 cm时,长方体纸盒的容积(A)
A.减少了$44 cm^3$
B.减少了$60 cm^3$
C.增加了$6 cm^3$
D.增加了$44 cm^3$

答案： 设剪去的小正方形边长为$x\,\text{cm}$，则折成的长方体纸盒底面边长为$(24 - 2x)\,\text{cm}$，高为$x\,\text{cm}$，容积$V=(24 - 2x)^2x$。
当$x = 4\,\text{cm}$时：
底面边长$=24 - 2×4=16\,\text{cm}$，
容积$V_1=16×16×4=1024\,\text{cm}^3$。
当$x = 5\,\text{cm}$时：
底面边长$=24 - 2×5=14\,\text{cm}$，
容积$V_2=14×14×5=980\,\text{cm}^3$。
容积变化量$V_1 - V_2=1024 - 980=44\,\text{cm}^3$，即容积减少了$44\,\text{cm}^3$。
A

8. 如图是一个正方体的表面展开图,如果相对面上所标的两个数互为相反数,那么x+y-z的值是(C)
A.1
B.7
C.9
D.3

答案： 解：将展开图还原成正方体，可得相对面为：2与y，3与z，-8与x。
因为相对面上的数互为相反数，所以：
y=-2，z=-3，x=8。
x+y-z=8+(-2)-(-3)=8-2+3=9。
答案：C