《2025年暑假总动员宁夏人民教育出版社七升八数学苏科版》

13. 如图,$AB // CD$,$BC // DE$,若$\angle B = 50^{\circ}$,则$\angle D$的度数是$130^{\circ}$。

答案： 解：因为 $AB // CD$，$\angle B = 50^{\circ}$，所以 $\angle C = \angle B = 50^{\circ}$（两直线平行，内错角相等）。
因为 $BC // DE$，所以 $\angle C + \angle D = 180^{\circ}$（两直线平行，同旁内角互补）。
所以 $\angle D = 180^{\circ} - \angle C = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
$130^{\circ}$

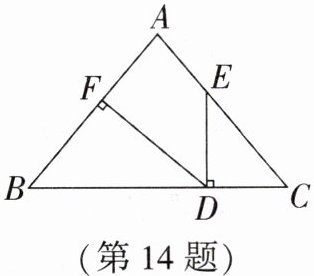
14. 如图,$\triangle ABC$中,$\angle B = \angle C$,$E是AC$上一点,$ED \perp BC$,$DF \perp AB$,垂足分别为$D$,$F$,若$\angle AED = 140^{\circ}$,则$\angle BDF = $40度。

答案： 解：
∵ $ED \perp BC$，$\angle AED = 140^\circ$，
∴ $\angle DEC = 180^\circ - \angle AED = 40^\circ$，
又
∵ $ED \perp BC$，$\angle EDC = 90^\circ$，
∴ $\angle C = 180^\circ - \angle EDC - \angle DEC = 180^\circ - 90^\circ - 40^\circ = 50^\circ$，
∵ $\angle B = \angle C$，
∴ $\angle B = 50^\circ$，
∵ $DF \perp AB$，$\angle DFB = 90^\circ$，
∴ $\angle BDF = 180^\circ - \angle DFB - \angle B = 180^\circ - 90^\circ - 50^\circ = 40^\circ$。
40

15. 如图,给出下列条件：①$\angle B + \angle BCD = 180^{\circ}$；②$\angle 1 = \angle 2$；③$\angle 3 = \angle 4$；④$\angle B = \angle 5$；⑤$\angle B = \angle D$。其中,一定能判定$AB // CD$的条件有①③④。(填写所有正确的序号)

答案： 解：①$\angle B + \angle BCD = 180^\circ$，同旁内角互补，两直线平行，可判定$AB // CD$；
②$\angle 1 = \angle 2$，内错角相等，两直线平行，判定的是$AD // BC$，不能判定$AB // CD$；
③$\angle 3 = \angle 4$，内错角相等，两直线平行，可判定$AB // CD$；
④$\angle B = \angle 5$，同位角相等，两直线平行，可判定$AB // CD$；
⑤$\angle B = \angle D$，不能判定$AB // CD$。
一定能判定$AB // CD$的条件有①③④。
答案：①③④

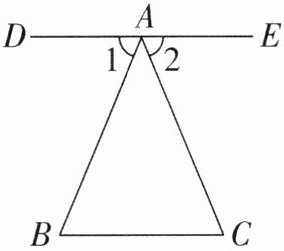
16. 如图,有下列三个条件：①$DE // BC$；②$\angle 1 = \angle 2$；③$\angle B = \angle C$。若从这三个条件中任选两个作为题设,另一个作为结论,组成一个命题,一共能组成3个真命题。

答案： 能组成的命题及证明如下：
命题1：若①②，则③.
证明：
∵DE//BC，
∴∠1=∠B，∠2=∠C.
∵∠1=∠2，
∴∠B=∠C.
命题2：若①③，则②.
证明：
∵DE//BC，
∴∠1=∠B，∠2=∠C.
∵∠B=∠C，
∴∠1=∠2.
命题3：若②③，则①.
证明：
∵∠1=∠2，∠B=∠C，且∠1+∠2+∠BAC=180°，∠B+∠C+∠BAC=180°，
∴∠1=∠B，
∴DE//BC.
综上，共3个真命题.
答案：3

17. (9分)写出下列命题的逆命题,并判断逆命题的真假。
(1)大于锐角的角是钝角；
(2)如果两个数的积为正数,那么这两个数都是正数；
(3)有限小数是有理数。

答案：
(1)逆命题：钝角是大于锐角的角。是真命题。
(2)逆命题：如果两个数都是正数，那么这两个数的积为正数。是真命题。
(3)逆命题：有理数是有限小数。是假命题。

18. (8分)下面的判断是否正确,为什么？
(1)对于所有的自然数$n$,$n^{2} + n$的值都是偶数；
(2)当$a \neq b$时,必有$ac^{2} \neq bc^{2}$。

答案：
(1)正确.
$\because n^{2}+n=n(n+1)$，$n$与$n+1$是两个连续自然数，必有一个为偶数，
$\therefore n(n+1)$是偶数，即$n^{2}+n$的值都是偶数.
(2)错误.
当$c=0$时，$ac^{2}=a×0=0$，$bc^{2}=b×0=0$，此时$ac^{2}=bc^{2}$.

19. (7分)如图,已知$D是\triangle ABC的外角平分线CD与BA$延长线的交点。求证：$\angle BAC ＞ \angle B$。

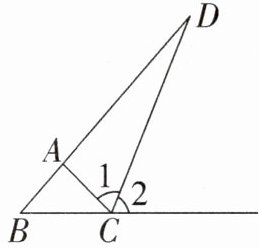
答案： 证明：
∵∠BAC是△ACD的外角，
∴∠BAC＞∠1（三角形的一个外角大于与它不相邻的任何一个内角）。
∵∠2是△BCD的外角，
∴∠2＞∠B（三角形的一个外角大于与它不相邻的任何一个内角）。
∵CD是△ABC的外角平分线，
∴∠1=∠2（角平分线定义）。
∴∠BAC＞∠2＞∠B，即∠BAC＞∠B。

20. (12分)(1)如图,$DE // BC$,$\angle 1 = \angle 3$,$CD \perp AB$。求证：$FG \perp AB$。
(2)若把(1)中的“$DE // BC$”与结论“$FG \perp AB$”对调,所得命题是否为真命题？试说明理由。
(3)若把(1)中的“$\angle 1 = \angle 3$”与结论“$FG \perp AB$”对调呢？

答案：
(1)证明：$\because DE// BC$，$\therefore \angle 1 = \angle 2$。
$\because \angle 1 = \angle 3$，$\therefore \angle 2 = \angle 3$，$\therefore CD// FG$。
$\therefore \angle BFG = \angle CDB$。
$\because CD\perp AB$，$\therefore \angle CDB = 90^\circ$，$\therefore \angle BFG = 90^\circ$，$\therefore FG\perp AB$。
(2)解：所得命题为真命题。
理由：$\because CD\perp AB$，$FG\perp AB$，$\therefore CD// FG$，$\therefore \angle 2 = \angle 3$。
$\because \angle 1 = \angle 3$，$\therefore \angle 1 = \angle 2$，$\therefore DE// BC$。
(3)解：所得命题为真命题。
理由：$\because CD\perp AB$，$FG\perp AB$，$\therefore CD// FG$，$\therefore \angle 2 = \angle 3$。
$\because DE// BC$，$\therefore \angle 1 = \angle 2$，$\therefore \angle 1 = \angle 3$。