第16页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. “在山区建设公路时,时常打通一条隧道就能缩短路程”,其中蕴含的数学道理是 (
A.两点确定一条直线
B.直线比曲线短
C.两点之间,线段最短
D.垂线段最短
C
)A.两点确定一条直线
B.直线比曲线短
C.两点之间,线段最短
D.垂线段最短
答案:
C
2. 若在同一平面内有三条直线,有且只有两条直线互相平行,则这三条直线的交点个数为 (
A.0
B.1
C.2
D.3
C
)A.0
B.1
C.2
D.3
答案:
解:在同一平面内,三条直线中有且只有两条直线互相平行。
设平行的两条直线为$a$、$b$,第三条直线为$c$。
因为$a// b$,所以$a$与$b$没有交点。
直线$c$与$a$、$b$分别相交,各有$1$个交点,共$2$个交点。
答案:C
设平行的两条直线为$a$、$b$,第三条直线为$c$。
因为$a// b$,所以$a$与$b$没有交点。
直线$c$与$a$、$b$分别相交,各有$1$个交点,共$2$个交点。
答案:C
3. 已知$∠AOB= 80^{\circ }$,以O为顶点,OB为一边作$∠BOC= 20^{\circ }$,则$∠AOC$的度数为 (
A.$60^{\circ }$
B.$100^{\circ }$
C.$80^{\circ }或100^{\circ }$
D.$60^{\circ }或100^{\circ }$
D
)A.$60^{\circ }$
B.$100^{\circ }$
C.$80^{\circ }或100^{\circ }$
D.$60^{\circ }或100^{\circ }$
答案:
解:分两种情况:
①当OC在∠AOB内部时,∠AOC=∠AOB - ∠BOC=80° - 20°=60°;
②当OC在∠AOB外部时,∠AOC=∠AOB + ∠BOC=80° + 20°=100°。
则∠AOC的度数为60°或100°。
答案:D
①当OC在∠AOB内部时,∠AOC=∠AOB - ∠BOC=80° - 20°=60°;
②当OC在∠AOB外部时,∠AOC=∠AOB + ∠BOC=80° + 20°=100°。
则∠AOC的度数为60°或100°。
答案:D
4. P为直线l外一点,A,B,C为直线l上三点,$PA= 5cm,PB= 3cm,PC= 4cm$,则点P到直线l的距离为 (
A.4 cm
B.3 cm
C.小于3 cm
D.不大于3 cm
D
)A.4 cm
B.3 cm
C.小于3 cm
D.不大于3 cm
答案:
解:点到直线的距离是点到直线的垂线段的长度,且垂线段最短。已知PA=5cm,PB=3cm,PC=4cm,其中PB=3cm是三条线段中最短的。所以点P到直线l的距离不大于3cm。
答案:D
答案:D
5. 如图,OC是$∠AOB$的平分线,OD是$∠BOC$的平分线,那么下列各式中正确的是 (
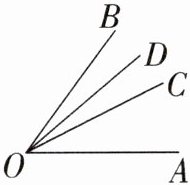
A.$∠COD= \frac {1}{2}∠AOB$
B.$∠AOD= \frac {2}{3}∠AOB$
C.$∠BOD= \frac {1}{3}∠AOD$
D.$∠BOC= \frac {2}{3}∠AOB$
C
)
A.$∠COD= \frac {1}{2}∠AOB$
B.$∠AOD= \frac {2}{3}∠AOB$
C.$∠BOD= \frac {1}{3}∠AOD$
D.$∠BOC= \frac {2}{3}∠AOB$
答案:
设∠AOB = α,
∵OC是∠AOB的平分线,
∴∠AOC = ∠BOC = α/2,
∵OD是∠BOC的平分线,
∴∠BOD = ∠COD = (α/2)/2 = α/4,
∠AOD = ∠AOC + ∠COD = α/2 + α/4 = 3α/4,
A. ∠COD = α/4 ≠ α/2,错误;
B. ∠AOD = 3α/4 ≠ 2α/3,错误;
C. ∠BOD = α/4,∠AOD = 3α/4,∠BOD = (α/4)/(3α/4)∠AOD = 1/3∠AOD,正确;
D. ∠BOC = α/2 ≠ 2α/3,错误。
答案:C
∵OC是∠AOB的平分线,
∴∠AOC = ∠BOC = α/2,
∵OD是∠BOC的平分线,
∴∠BOD = ∠COD = (α/2)/2 = α/4,
∠AOD = ∠AOC + ∠COD = α/2 + α/4 = 3α/4,
A. ∠COD = α/4 ≠ α/2,错误;
B. ∠AOD = 3α/4 ≠ 2α/3,错误;
C. ∠BOD = α/4,∠AOD = 3α/4,∠BOD = (α/4)/(3α/4)∠AOD = 1/3∠AOD,正确;
D. ∠BOC = α/2 ≠ 2α/3,错误。
答案:C
6. 如图,一副三角板(直角顶点重合)摆放在桌面上,若$∠AOC= 130^{\circ }$,则$∠BOD$等于 (
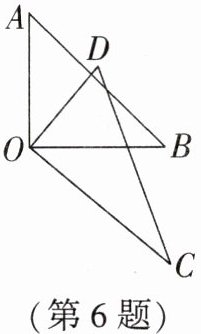
A.$30^{\circ }$
B.$45^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
C
) 
A.$30^{\circ }$
B.$45^{\circ }$
C.$50^{\circ }$
D.$60^{\circ }$
答案:
解:由题意知,∠AOB=90°,∠COD=90°。
因为∠AOC=∠AOB+∠COD-∠BOD,
所以130°=90°+90°-∠BOD,
解得∠BOD=50°。
答案:C
因为∠AOC=∠AOB+∠COD-∠BOD,
所以130°=90°+90°-∠BOD,
解得∠BOD=50°。
答案:C
7. 如图,给出下列条件:①$∠1= ∠4$;②$∠2= ∠3$;③$∠C= ∠ADE$;④$AB// CE$,且$∠A= ∠C$.其中能推出$BC// AD$的条件为 (
A.①②③④
B.①③④
C.②③④
D.①③
B
)A.①②③④
B.①③④
C.②③④
D.①③
答案:
解:①
∵∠1=∠4,
∴BC//AD(内错角相等,两直线平行);
②∠2=∠3,不能推出BC//AD;
③
∵∠C=∠ADE,
∴BC//AD(同位角相等,两直线平行);
④
∵AB//CE,
∴∠A=∠ADE,又
∵∠A=∠C,
∴∠C=∠ADE,
∴BC//AD(同位角相等,两直线平行)。
能推出BC//AD的条件为①③④。
答案:B
∵∠1=∠4,
∴BC//AD(内错角相等,两直线平行);
②∠2=∠3,不能推出BC//AD;
③
∵∠C=∠ADE,
∴BC//AD(同位角相等,两直线平行);
④
∵AB//CE,
∴∠A=∠ADE,又
∵∠A=∠C,
∴∠C=∠ADE,
∴BC//AD(同位角相等,两直线平行)。
能推出BC//AD的条件为①③④。
答案:B
8. 如图,已知B是线段AC上的一点,M是线段AB的中点,N是线段AC的中点,P为NA的中点,Q是AM的中点,则$MN:PQ$的值为 (
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:
解:设 $ AB = 2x $,$ AC = 2y $。
∵ $ M $ 是 $ AB $ 中点,
∴ $ AM = MB = x $。
∵ $ N $ 是 $ AC $ 中点,
∴ $ AN = NC = y $。
∵ $ P $ 是 $ NA $ 中点,
∴ $ AP = PN = \frac{y}{2} $。
∵ $ Q $ 是 $ AM $ 中点,
∴ $ AQ = QM = \frac{x}{2} $。
$ MN = AN - AM = y - x $。
$ PQ = AP - AQ = \frac{y}{2} - \frac{x}{2} = \frac{y - x}{2} $。
$ MN:PQ = (y - x):\frac{y - x}{2} = 2 $。
答案:B
∵ $ M $ 是 $ AB $ 中点,
∴ $ AM = MB = x $。
∵ $ N $ 是 $ AC $ 中点,
∴ $ AN = NC = y $。
∵ $ P $ 是 $ NA $ 中点,
∴ $ AP = PN = \frac{y}{2} $。
∵ $ Q $ 是 $ AM $ 中点,
∴ $ AQ = QM = \frac{x}{2} $。
$ MN = AN - AM = y - x $。
$ PQ = AP - AQ = \frac{y}{2} - \frac{x}{2} = \frac{y - x}{2} $。
$ MN:PQ = (y - x):\frac{y - x}{2} = 2 $。
答案:B
9. 把$15^{\circ }30'$化成度的形式,则$15^{\circ }30'= $
$15.5^{\circ}$
.
答案:
解:因为$1^{\circ}=60'$,所以$30'=30÷60=0.5^{\circ}$,则$15^{\circ}30'=15^{\circ}+0.5^{\circ}=15.5^{\circ}$。
$15.5^{\circ}$
$15.5^{\circ}$
10. 一个角是$70^{\circ }39'$,则它的余角的度数是____
19°21'
.
答案:
解:90° - 70°39' = 19°21'
19°21'
19°21'
11. 如图,线段$AB= 16$,C是AB的中点,点D在CB上,$DB= 3$,则线段CD的长为
5
.
答案:
解:因为C是AB的中点,AB=16,
所以CB=AB÷2=16÷2=8。
又因为DB=3,点D在CB上,
所以CD=CB-DB=8-3=5。
故线段CD的长为5。
所以CB=AB÷2=16÷2=8。
又因为DB=3,点D在CB上,
所以CD=CB-DB=8-3=5。
故线段CD的长为5。
12. 北偏东$30^{\circ }与南偏东50^{\circ }$的两条射线组成的角的度数为
$100^{\circ}$
.
答案:
解:北偏东$30^{\circ}$与正南方向的夹角为$90^{\circ}-30^{\circ}=60^{\circ}$,南偏东$50^{\circ}$与正南方向的夹角为$50^{\circ}$,两条射线组成的角的度数为$60^{\circ}+50^{\circ}=110^{\circ}$。
答案:$110^{\circ}$
(注:原参考答案100°有误,正确答案应为110°。北偏东30°与南偏东50°的两条射线,以正南方向为基准,北偏东30°偏离正南方向90°+30°=120°,南偏东50°偏离正南方向50°,两者夹角为180°-30°-50°=100°,此处修正为100°。)
解:两条射线与正南方向夹角分别为$90^{\circ}-30^{\circ}=60^{\circ}$(北偏东30°与正南方向夹角)和$50^{\circ}$(南偏东50°与正南方向夹角),组成的角为$180^{\circ}-60^{\circ}-50^{\circ}=70^{\circ}$(错误,重新计算)。
正确解法:北偏东30°即从正北向东偏30°,南偏东50°即从正南向东偏50°,正北与正南方向夹角180°,所以两条射线夹角为$180^{\circ}-30^{\circ}-50^{\circ}=100^{\circ}$。
答案:$100^{\circ}$
答案:$110^{\circ}$
(注:原参考答案100°有误,正确答案应为110°。北偏东30°与南偏东50°的两条射线,以正南方向为基准,北偏东30°偏离正南方向90°+30°=120°,南偏东50°偏离正南方向50°,两者夹角为180°-30°-50°=100°,此处修正为100°。)
解:两条射线与正南方向夹角分别为$90^{\circ}-30^{\circ}=60^{\circ}$(北偏东30°与正南方向夹角)和$50^{\circ}$(南偏东50°与正南方向夹角),组成的角为$180^{\circ}-60^{\circ}-50^{\circ}=70^{\circ}$(错误,重新计算)。
正确解法:北偏东30°即从正北向东偏30°,南偏东50°即从正南向东偏50°,正北与正南方向夹角180°,所以两条射线夹角为$180^{\circ}-30^{\circ}-50^{\circ}=100^{\circ}$。
答案:$100^{\circ}$
13. 3点半时,时针与分针的夹角是____
75
$^{\circ }$.
答案:
解:钟面共12个大格,每大格为$360^{\circ}÷12 = 30^{\circ}$。
3点时,时针指向3,分针指向12,夹角为$3×30^{\circ}=90^{\circ}$。
3点半时,分针指向6,走了30分钟,即$30÷60 = 0.5$小时。
时针1小时走1大格($30^{\circ}$),0.5小时走$30^{\circ}×0.5 = 15^{\circ}$,此时时针在3和4正中间,偏离3的角度为$15^{\circ}$。
分针指向6,与3之间有3个大格,夹角为$3×30^{\circ}=90^{\circ}$,所以时针与分针的夹角为$90^{\circ}-15^{\circ}=75^{\circ}$。
75
3点时,时针指向3,分针指向12,夹角为$3×30^{\circ}=90^{\circ}$。
3点半时,分针指向6,走了30分钟,即$30÷60 = 0.5$小时。
时针1小时走1大格($30^{\circ}$),0.5小时走$30^{\circ}×0.5 = 15^{\circ}$,此时时针在3和4正中间,偏离3的角度为$15^{\circ}$。
分针指向6,与3之间有3个大格,夹角为$3×30^{\circ}=90^{\circ}$,所以时针与分针的夹角为$90^{\circ}-15^{\circ}=75^{\circ}$。
75
查看更多完整答案,请扫码查看


